
分析 (1)当a=1时,f(x)=lg$\frac{x-1}{x+4}$,利用导数法即可得出结论;
(2)假设存在,利用奇函数的定义,即可得出结论.
解答 解:(1)当a=1时,f(x)=lg$\frac{x-1}{x+4}$,
令y=$\frac{x-1}{x+4}$,则y′=$\frac{5}{(x+4)^{2}}$>0,即函数y=$\frac{x-1}{x+4}$,在(1,+∞)上单调递增,
∴函数y=f(x)在(1,+∞)上单调递增;
(2)f(-x)=lg$\frac{-x+1-2a}{-x+1+3a}$,f(-x)+f(x)=0,
可得(x-1+2a)(x+1-2a)=(x-1-3a)(x+1+3a),
∴a=-2,函数是奇函数.
点评 本题考查函数的奇偶性,考查增函数的判断,考查导数法,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
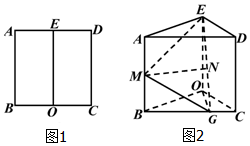 如图1,在边长为$2\sqrt{3}$的正方形ABCD中,E、O分别为 AD、BC的中点,沿 EO将矩形ABOE折起使得∠BOC=120°,如图2,点G 在BC上,BG=2GC,M、N分别为AB、EG中点.
如图1,在边长为$2\sqrt{3}$的正方形ABCD中,E、O分别为 AD、BC的中点,沿 EO将矩形ABOE折起使得∠BOC=120°,如图2,点G 在BC上,BG=2GC,M、N分别为AB、EG中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com