
【题目】已知复数z=![]() ,(m∈R,i是虚数单位).
,(m∈R,i是虚数单位).
(1)若z是纯虚数,求m的值;
(2)设![]() 是z的共轭复数,复数
是z的共轭复数,复数![]() +2z在复平面上对应的点在第一象限,求m的取值范围.
+2z在复平面上对应的点在第一象限,求m的取值范围.
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:(1)化简z=1-2m+(2m+1)i,若z是纯虚数,只需1-2m=0且2m+1≠0即可;
(2)求得![]() 1-2m-(2m+1)i,得
1-2m-(2m+1)i,得![]() +2z=3-6m+(2m+1)i,只需
+2z=3-6m+(2m+1)i,只需![]() 即可.
即可.
试题解析:
(1)z=![]() =
=![]()
=1-2m+(2m+1)i.
因为z是纯虚数,所以1-2m=0且2m+1≠0,
解得m=![]() .
.
(2)因为![]() 是z的共轭复数,所以
是z的共轭复数,所以![]() =1-2m-(2m+1)i.
=1-2m-(2m+1)i.
所以![]() +2z=1-2m-(2m+1)i+2[1-2m+(2m+1)i]
+2z=1-2m-(2m+1)i+2[1-2m+(2m+1)i]
=3-6m+(2m+1)i.
因为复数![]() +2z在复平面上对应的点在第一象限,
+2z在复平面上对应的点在第一象限,
所以![]()
解得-![]() <m<
<m<![]() ,即实数m的取值范围为(-
,即实数m的取值范围为(-![]() ,
,![]() ).
).
点睛:形如![]() 的数叫复数,其中a叫做复数的实部,b叫做复数的虚部.
的数叫复数,其中a叫做复数的实部,b叫做复数的虚部.
当![]() 时复数
时复数![]() 为实数,
为实数,
当![]() 时复数
时复数![]() 为虚数,
为虚数,
当![]() 时复数
时复数![]() 为纯虚数.
为纯虚数.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右顶点是双曲线
的左右顶点是双曲线![]() 的顶点,且椭圆
的顶点,且椭圆![]() 的上顶点到双曲线
的上顶点到双曲线![]() 的渐近线的距离为
的渐近线的距离为![]() 。
。
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与
与![]() 相交于
相交于![]() 两点,与
两点,与![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某专营店经销某商品,当售价不高于10元时,每天能销售100件,当价格高于10元时,每提高1元,销量减少3件,若该专营店每日费用支出为500元,用x表示该商品定价,y表示该专营店一天的净收入(除去每日的费用支出后的收入).
(1)把y表示成x的函数;
(2)试确定该商品定价为多少元时,一天的净收入最高?并求出净收入的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),且直线
为参数),且直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,以直角坐标系的原点为极点,以
两点,以直角坐标系的原点为极点,以![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2) 已知点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一年级学生全部参加了体育科目的达标测试,现从中随机抽取40名学生的测试成
绩,整理数据并按分数段![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 进行分
进行分
组,已知测试分数均为整数,现用每组区间的中点值代替该组中的每个数据,则得到体育成绩的折
线图如下:
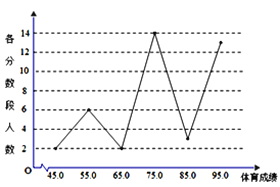
(1)若体育成绩大于或等于70分的学生为“体育良好”,已知该校高一年级有1000名学生,试估计该校高一年级学生“体育良好”的人数;
(2)为分析学生平时的体育活动情况,现从体育成绩在![]() 和
和![]() 的样本学生中随机抽取2人,求所抽取的2名学生中,至少有1人为“体育良好”的概率;
的样本学生中随机抽取2人,求所抽取的2名学生中,至少有1人为“体育良好”的概率;
(3)假设甲、乙、丙三人的体育成绩分别为![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,
![]() ,当三人的体育成绩方差
,当三人的体育成绩方差![]() 最小时,写出
最小时,写出![]() ,
,![]() ,
,![]() 的值(不要求证明).
的值(不要求证明).
注:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)求函数![]() 在区间
在区间![]() 上的值域
上的值域
(2)把函数![]() 图象所有点的上横坐标缩短为原来的
图象所有点的上横坐标缩短为原来的![]() 倍,再把所得的图象向左平移
倍,再把所得的图象向左平移![]() 个单位长度
个单位长度![]() ,再把所得的图象向下平移1个单位长度,得到函数
,再把所得的图象向下平移1个单位长度,得到函数![]() , 若函数
, 若函数![]() 关于点
关于点![]() 对称
对称
(i)求函数![]() 的解析式;
的解析式;
(ii)求函数![]() 单调递增区间及对称轴方程.
单调递增区间及对称轴方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,求曲线
,求曲线![]() 在点
在点![]() 处的切线;
处的切线;
(2)若函数![]() 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数![]() 的取值范围;
的取值范围;
(3)设函数![]() ,若在
,若在![]() 上至少存在一点
上至少存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com