
【题目】如图甲,直角梯形![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 分别在
分别在![]() 上,且
上,且![]() ,
, ![]() ,
, ![]() ,现将梯形
,现将梯形![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 与平面
与平面![]() 垂直(如图乙).
垂直(如图乙).
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
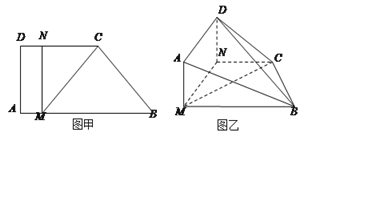
(II)当![]() 的长为何值时,二面角
的长为何值时,二面角![]() 的大小为
的大小为![]() ?
?
【答案】(Ⅰ)见解析;(Ⅱ) ![]() .
.
【解析】试题分析:
(1)建立空间直角坐标系,结合直线的方向向量和平面的一个法向量即可证得线面平行;
(2)结合空间直角坐标系探究可得![]() 时,二面角
时,二面角![]() 的大小为
的大小为![]() .
.
试题解析:
(Ⅰ)如图建立空间直角坐标系N-xyz.
设![]() ,则A(2,0,t),B(2,4,0),
,则A(2,0,t),B(2,4,0), ![]()
又易知平面DNC的一个法向量为![]() ,
,
由![]() ,得AB∥平面DNC.
,得AB∥平面DNC.
(Ⅱ)设![]() ,则D(0,0,t),C(0,2,0),B(2,4,0),故
,则D(0,0,t),C(0,2,0),B(2,4,0),故![]() (0,-2,t),
(0,-2,t), ![]() (2,2,0),
(2,2,0),
设平面DBC的一个法向量为![]() ,则
,则![]()
取![]() ,则
,则![]() ,即
,即![]() ,
,
又易知平面BCN的一个法向量为![]() ,
,
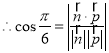 ,即
,即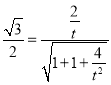 ,解得
,解得![]() .
.
另解:(Ⅰ)∵MB∥NC,MB![]() 平面DNC,NC
平面DNC,NC![]() 平面DNC,
平面DNC,
∴MB∥平面DNC. 同理MA∥平面DNC,
又MA∩MB=M且MA、MB![]() 平面MAB,
平面MAB,
∴平面MAB∥平面NCD, 又AB![]() 平面MAB,
平面MAB,
∴AB∥平面NCD.
(Ⅱ)过N作NH⊥BC交BC延长线于H,连结DH,
∵平面AMND⊥平面MNCB,DN⊥MN
∴DN⊥平面MNCB,从而DH⊥BC,
∴∠DHN为二面角D-BC-N的平面角.
由已知得, ![]() ,∴
,∴![]() ,
, ![]() ,
,
∴![]() .
.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:
【题目】抛物线C:y2=2px(p>0)的准线为l,焦点为F.⊙M的圆心在x轴的正半轴上,且与y轴相切.过原点O作倾斜角为![]() 的直线n交l于点A, 交⊙M于另一点B,且AO=OB=2.
的直线n交l于点A, 交⊙M于另一点B,且AO=OB=2.
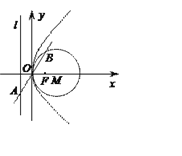
(1)求⊙M和抛物线C的方程;
(2)若P为抛物线C上的动点,求![]() 的最小值;
的最小值;
(3)过l上的动点Q向⊙M作切线,切点为S,T,求证:直线ST恒过一个定点,并求该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合M={(x,y)|y=f(x)},若对于任意(x1,y1)∈M,存在(x2,y2)∈M,使得x1x2+y1y2=0成立,则称集合M是“垂直对点集”.给出下列四个集合:
①M={![]() };②M={(x,y)|y=sinx+1};
};②M={(x,y)|y=sinx+1};
③M={(x,y)|y=log2x};④M={(x,y)|y=ex﹣2}.
其中是“垂直对点集”的序号是( )
A. ①② B. ②③ C. ①④ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C的一个焦点为![]() ,对应于这个焦点的准线方程为
,对应于这个焦点的准线方程为![]()
(1)写出抛物线C的方程;
(2)过F点的直线与曲线C交于A、B两点,O点为坐标原点,求△AOB重心G的轨迹方程;
(3)点P是抛物线C上的动点,过点P作圆![]() 的切线,切点分别是M,N.当P点在何处时,|MN|的值最小?求出|MN|的最小值.
的切线,切点分别是M,N.当P点在何处时,|MN|的值最小?求出|MN|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “![]() 为真”是“
为真”是“![]() 为真”的充分不必要条件;
为真”的充分不必要条件;
B. 样本![]() 的标准差是3.3;
的标准差是3.3;
C. K2是用来判断两个分类变量是否相关的随机变量,当K2的值很小时可以推定两类变量不相关;
D. 设有一个回归直线方程为![]() ,则变量
,则变量![]() 每增加一个单位,
每增加一个单位,![]() 平均减少1.5个单位.
平均减少1.5个单位.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=lg(ax﹣bx),且f(1)=lg2,f(2)=lg12
(1)求a,b的值.
(2)当x∈[1,2]时,求f(x)的最大值.
(3)m为何值时,函数g(x)=ax的图象与h(x)=bx﹣m的图象恒有两个交点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.
(1)求顾客抽奖1次能获奖的概率;
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com