
【题目】某玩具厂生产出一种新型儿童泡沫玩具飞机,为更精确的确定最终售价,该厂采用了多种价格对该玩具飞机进行了试销,某销售点的销售情况如下表:
单价 | 8 | 9 | 10 | 11 | 12 |
销量 | 40 | 36 | 30 | 24 | 20 |
从散点图可以看出,这些点大致分布在一条直线的附近,变量![]() ,
,![]() 有较强的线性相关性.
有较强的线性相关性.
(1)求销量![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)若每架该玩具飞机的成本价为5元,利用(1)的结果,预测每架该玩具飞机的定价为多少元时,总利润最大.(结果保留一位小数)
(附: ,
,![]() ,
,![]() ,
,![]() .)
.)
科目:高中数学 来源: 题型:
【题目】自2017年2月底,90多所自主招生试点高校将陆续出台2017年自主招生简章,某校高三年级选取了在期中考试中成绩优异的100名学生作为调查对象,对是否准备参加2017年的自主招生考试进行了问卷调查,其中“准备参加”“不准备参加”和“待定”的人数如表:
准备参加 | 不准备参加 | 待定 | |
男生 | 30 | 6 | 15 |
女生 | 15 | 9 | 25 |
(1)在所有参加调查的同学中,在三种类型中用分层抽样的方法抽取20人进行座谈交流,则在“准备参加”“不准备参加”和“待定”的同学中应各抽取多少人?
(2)在“准备参加”的同学中用分层抽样方法抽取6人,从这6人中任意抽取2人,求至少有一名女生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一半径为2米的水轮如图所示,水轮圆心![]() 距离水面1米;已知水轮按逆时针做匀速转动,每3秒转一圈,如果当水轮上点
距离水面1米;已知水轮按逆时针做匀速转动,每3秒转一圈,如果当水轮上点![]() 从水中浮现时(图中点
从水中浮现时(图中点![]() )开始计算时间.
)开始计算时间.
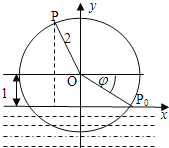
(1)试将点![]() 距离水面的高度
距离水面的高度![]() (单位:米)表示为时间
(单位:米)表示为时间![]() (单位:秒)的函数
(单位:秒)的函数![]() ;
;
(2)点![]() 第一次到达最高点大约要多长时间?
第一次到达最高点大约要多长时间?
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】伴随着智能手机的深入普及,支付形式日渐多样化,打破了传统支付的局限性和壁垒,有研究表明手机支付的使用比例与人的年龄存在一定的关系,某调研机构随机抽取了50人,对他们一个月内使用手机支付的情况进行了统计,如下表:

(1)若以“年龄55岁为分界点”,由以上统计数据完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为“使用手机支付”与人的年龄有关;
的把握认为“使用手机支付”与人的年龄有关;

(2)若从年龄在![]() ,
,![]() 内的被调查人中各随机选取2人进行追踪调查,记选中的4人中“使用手机支付”的人数为
内的被调查人中各随机选取2人进行追踪调查,记选中的4人中“使用手机支付”的人数为![]() .
.
①求随机变量![]() 的分布列;
的分布列;
②求随机变量![]() 的数学期望.
的数学期望.
参考数据如下:
| 0.05 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
参考格式:![]() ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人在相同的条件下投篮5轮,每轮甲、乙各投篮10次,投篮命中次数的情况如图所示(实线为甲的折线图,虚线为乙的折线图),则以下说法错误的是( )

A. 甲投篮命中次数的众数比乙的小
B. 甲投篮命中次数的平均数比乙的小
C. 甲投篮命中次数的中位数比乙的大
D. 甲投篮命中的成绩比乙的稳定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为梯形,
为梯形,![]() ,
,![]() .
.![]() 是
是![]() 的中点,
的中点,![]() 底面
底面![]() ,
,![]() 在平面
在平面![]() 上的正投影为点
上的正投影为点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() .
.
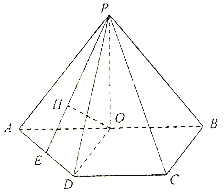
(1)求证:![]() 为
为![]() 中点;
中点;
(2)若![]() ,
,![]() ,在棱
,在棱![]() 上确定一点
上确定一点![]() ,使得
,使得![]() 平面
平面![]() ,并求出
,并求出![]() 与面
与面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游区每年各个月份接待游客的人数近似地满足周期性规律,因而第![]() 个月从事旅游服务工作的人数
个月从事旅游服务工作的人数![]() 可近似地用函数
可近似地用函数![]() 来刻画,其中正整数
来刻画,其中正整数![]() 表示月份且
表示月份且![]() ,例如
,例如![]() 表示1月份,
表示1月份,![]() 和
和![]() 是正整数,
是正整数,![]() ,
,![]() . 统计发现,该地区每年各个月份从事旅游服务工作的人数有以下规律:
. 统计发现,该地区每年各个月份从事旅游服务工作的人数有以下规律:
① 每年相同的月份,该地区从事旅游服务工作的人数基本相同;
② 该地区从事旅游服务工作的人数最多的8月份和最少的2月份相差400人;
③ 2月份该地区从事旅游服务工作的人数为100人,随后逐月递增直到8月份达到最多.
(1)试根据已知信息,求![]() 的表达式;
的表达式;
(2)一般地,当该地区从事旅游服务工作的人数在400或400以上时,该地区也进入了一年中的旅游“旺季”,那么,一年中的哪几个月是该地区的旅游“旺季”?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车因绿色、环保、健康的出行方式,在国内得到迅速推广.最近,某机构在某地区随机采访了10名男士和10名女士,结果男士、女士中分别有7人、6人表示“经常骑共享单车出行”,其他人表示“较少或不选择骑共享单车出行”.
(1)从这些男士和女士中各抽取一人,求至少有一人“经常骑共享单车出行”的概率;
(2)从这些男士中抽取一人,女士中抽取两人,记这三人中“经常骑共享单车出行”的人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的图象为
的图象为![]() ,则以下结论中正确的是__________.(写出所有正确结论的编号)
,则以下结论中正确的是__________.(写出所有正确结论的编号)
①图象![]() 关于直线
关于直线![]() 对称;
对称;
②图象![]() 关于点
关于点![]() 对称;
对称;
③函数![]() 在区间
在区间![]() 内是增函数;
内是增函数;
④由![]() 的图象向右平移
的图象向右平移![]() 个单位长度可以得到图象
个单位长度可以得到图象![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com