
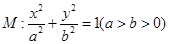 的离心率为
的离心率为 ,且过点
,且过点 直线
直线 与椭圆M交于A、C两点,直线
与椭圆M交于A、C两点,直线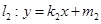 与椭圆M交于B、D两点,四边形ABCD是平行四边形
与椭圆M交于B、D两点,四边形ABCD是平行四边形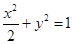 ;(2)详见解析;(3)最小值为
;(2)详见解析;(3)最小值为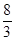
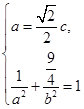 ,再加上
,再加上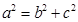 ,解此方程组即可得
,解此方程组即可得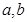 的值,从而得椭圆
的值,从而得椭圆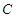 的方程(2)由于四边形ABCD是平行四边形,所以ABCD的对角线AC和BD的中点重合
的方程(2)由于四边形ABCD是平行四边形,所以ABCD的对角线AC和BD的中点重合 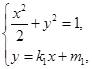 消去
消去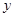 得:
得: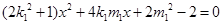 ,显然点A、C的横坐标是这个方程的两个根,由此可得线段
,显然点A、C的横坐标是这个方程的两个根,由此可得线段 的中点为
的中点为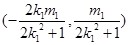 同理可得线段
同理可得线段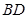 的中点为
的中点为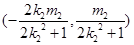 ,由于中点重合,所以
,由于中点重合,所以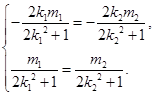 ,解得:
,解得: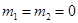 或
或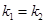 (舍)这说明
(舍)这说明 和
和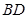 都过原点即相交于原点
都过原点即相交于原点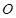 (3)由于对角线过原点且该四边形为菱形,所以其面积为
(3)由于对角线过原点且该四边形为菱形,所以其面积为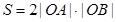 由方程组
由方程组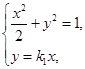 易得点A的坐标(用
易得点A的坐标(用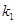 表示),从而得
表示),从而得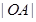 (用
(用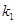 表示);同理可得
表示);同理可得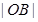 (由于
(由于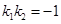 ,故仍可用
,故仍可用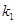 表示)这样就可将
表示)这样就可将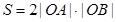 表示为
表示为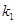 的函数,从而求得其最小值
的函数,从而求得其最小值 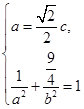 ,又因为
,又因为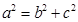 ,所以得
,所以得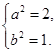
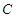 的方程为
的方程为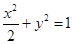 3分
3分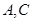 满足
满足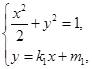
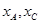 是方程
是方程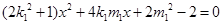 的两个根
的两个根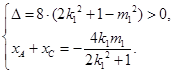
 的中点为
的中点为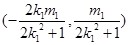
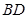 的中点为
的中点为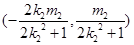 5分
5分 是平行四边形,所以
是平行四边形,所以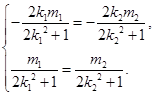
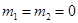 或
或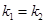 (舍)
(舍) 的对角线
的对角线 和
和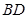 相交于原点
相交于原点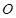 7分
7分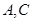 满足
满足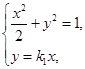
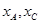 是方程
是方程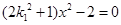 的两个根,即
的两个根,即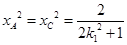
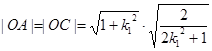
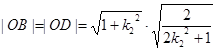 9分
9分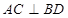 ,所以
,所以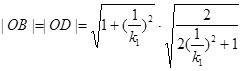 ,其中
,其中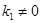
 的面积
的面积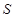 为
为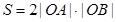
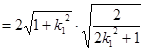
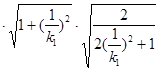 ,
, 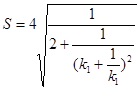 ,其中
,其中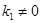 10分
10分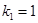 或
或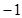 时,菱形
时,菱形 的面积最小,该最小值为
的面积最小,该最小值为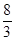 12分
12分

 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源:不详 题型:解答题
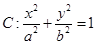
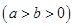 的右焦点
的右焦点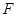
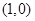 ,长轴的左、右端点分别为
,长轴的左、右端点分别为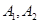 ,且
,且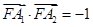 .
.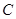 的方程;
的方程;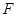 斜率为
斜率为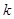 (
( )的直线
)的直线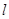 交椭圆
交椭圆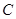 于
于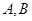 两点,弦
两点,弦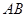 的垂直平分线与
的垂直平分线与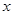 轴相交于
轴相交于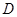 点. 试问椭圆
点. 试问椭圆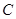 上是否存在点
上是否存在点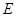 使得四边形
使得四边形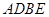 为菱形?若存在,求
为菱形?若存在,求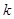 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
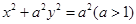 的一个顶点
的一个顶点 为直角顶点作此椭圆的内接等腰直角三角形
为直角顶点作此椭圆的内接等腰直角三角形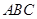 ,试问:(1)这样的等腰直角三角形是否存在?若存在,写出一个等腰直角三角形两腰所在的直线方程。若不存在,说明理由。(2)这样的等腰直角三角形若存在,最多有几个?
,试问:(1)这样的等腰直角三角形是否存在?若存在,写出一个等腰直角三角形两腰所在的直线方程。若不存在,说明理由。(2)这样的等腰直角三角形若存在,最多有几个?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
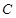 :
: (
(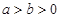 )的焦距为
)的焦距为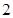 ,且过点(
,且过点(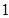 ,
,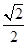 ),右焦点为
),右焦点为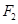 .设
.设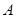 ,
,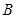 是
是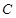 上的两个动点,线段
上的两个动点,线段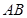 的中点
的中点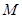 的横坐标为
的横坐标为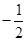 ,线段
,线段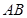 的中垂线交椭圆
的中垂线交椭圆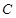 于
于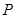 ,
,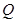 两点.
两点.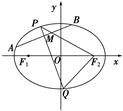
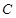 的方程;
的方程;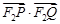 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ),且长轴长与短轴长的比是
),且长轴长与短轴长的比是 ∶1.
∶1.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
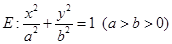 的左焦点为
的左焦点为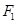 ,右焦点为
,右焦点为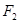 ,过
,过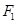 的直线交椭圆于
的直线交椭圆于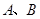 两点,
两点,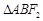 的周长为8,且
的周长为8,且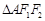 面积最大时,
面积最大时,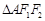 为正三角形.
为正三角形.
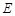 的方程;
的方程;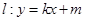 与椭圆
与椭圆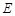 有且只有一个公共点
有且只有一个公共点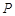 ,且与直线
,且与直线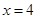 相交于点
相交于点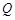 ,证明:点
,证明:点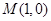 在以
在以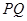 为直径的圆上.
为直径的圆上.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
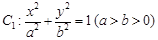 的离心率为
的离心率为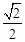 ,
,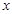 轴被曲线
轴被曲线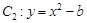 截得的线段长等于
截得的线段长等于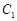 的短轴长。
的短轴长。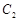 与
与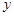 轴的交点为
轴的交点为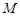 ,过坐标原点
,过坐标原点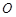 的直线
的直线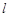 与
与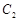 相交于点
相交于点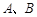 ,直线
,直线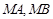 分别与
分别与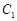 相交于点
相交于点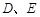 。
。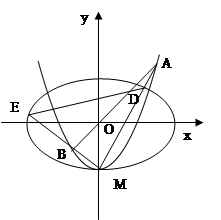
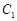 、
、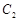 的方程;
的方程;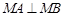 。
。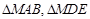 的面积分别为
的面积分别为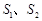 ,若
,若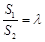 ,求
,求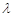 的取值范围。
的取值范围。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 与椭圆
与椭圆 中心在原点,焦点均在
中心在原点,焦点均在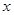 轴上,且离心率相同.椭圆
轴上,且离心率相同.椭圆 的长轴长为
的长轴长为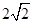 ,且椭圆
,且椭圆 的左准线
的左准线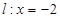 被椭圆
被椭圆 截得的线段
截得的线段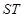 长为
长为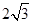 ,已知点
,已知点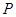 是椭圆
是椭圆 上的一个动点.
上的一个动点.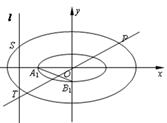
 与椭圆
与椭圆 的方程;
的方程;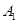 为椭圆
为椭圆 的左顶点,点
的左顶点,点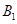 为椭圆
为椭圆 的下顶点,若直线
的下顶点,若直线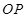 刚好平分
刚好平分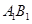 ,求点
,求点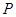 的坐标;
的坐标;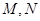 在椭圆
在椭圆 上,点
上,点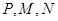 满足
满足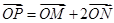 ,则直线
,则直线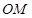 与直线
与直线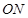 的斜率之积是否为定值?若是,求出该定值;若不是,说明理由.
的斜率之积是否为定值?若是,求出该定值;若不是,说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com