

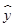 =bx+a必过的点是
=bx+a必过的点是| A.(2,2) | B.(1,2) | C.(3,4) | D.(4,5) |
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
| 身高(cm) | [160,165) | [165,170) | [170,175) | [175,180) | [180,185) | [185,190) |
| 频数 | 2 | 5 | 14 | 13 | 4 | 2 |
| 身高(cm) | [150,155) | [155,160) | [160,165) | [165,170) | [170,175) | [175,180) |
| 频数 | 1 | 7 | 12 | 6 | 3 | 1 |

 的概率;
的概率; 190cm之间的男生中任选2人,求至少有1人身高在185
190cm之间的男生中任选2人,求至少有1人身高在185 190cm之间的概率。
190cm之间的概率。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 性别 科目 | 男 | 女 |
| 文科 | 2 | 5 |
| 理科 | 10 | 3 |
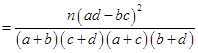 (其中
(其中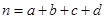 ))
))查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 列联表得出
列联表得出 ,故有 把握认为婴儿的性别与出生时间有关系(利用下表解决问题)( )
,故有 把握认为婴儿的性别与出生时间有关系(利用下表解决问题)( )
A. | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 高一成绩x | 74 | 71 | 72 | 68 | 76 | 73 | 67 | 70 | 65 | 74 |
| 高二成绩y | 76 | 75 | 71 | 70 | 76 | 79 | 65 | 77 | 62 | 72 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| 单价 (元/kg) | 2 | 2.4 | 2.8 | 3.2 | 3.6 | 4 | 单价 (元/kg) | 4 | 3.4 | 2.9 | 2.6 | 2.3 | 2 |
| 供给量 (1000kg) | 50 | 60 | 70 | 75 | 80 | 90 | 需求量 (1000kg) | 50 | 60 | 65 | 70 | 75 | 80 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com