
平面内与两定点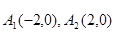 连线的斜率之积等于非零常数
连线的斜率之积等于非零常数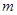 的点的轨迹,加上
的点的轨迹,加上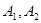 两点,所成的曲线
两点,所成的曲线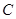 可以是圆,椭圆或双曲线.
可以是圆,椭圆或双曲线.
(Ⅰ)求曲线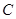 的方程,并讨论
的方程,并讨论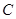 的形状与
的形状与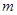 值的关系;
值的关系;
(Ⅱ)当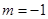 时,对应的曲线为
时,对应的曲线为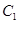 ;对给定的
;对给定的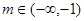 ,对应的曲线为
,对应的曲线为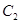 ,若曲线
,若曲线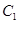 的斜率为
的斜率为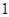 的切线与曲线
的切线与曲线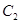 相交于
相交于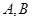 两点,且
两点,且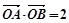 (
(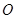 为坐标原点),求曲线
为坐标原点),求曲线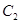 的方程.
的方程.
(Ⅰ)当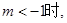 曲线
曲线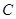 的方程为
的方程为 ,
,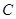 是焦点在
是焦点在 轴上的椭圆;
轴上的椭圆;
当 时,曲线
时,曲线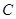 的方程为
的方程为 ,
,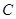 是圆心在原点,半径为2的圆;
是圆心在原点,半径为2的圆;
当 时,曲线
时,曲线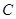 的方程为
的方程为 ,
,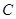 是焦点在
是焦点在 轴上的椭圆;
轴上的椭圆;
当 时,曲线
时,曲线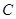 的方程为
的方程为 ,
,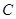 是焦点在
是焦点在 轴上的双曲线.
轴上的双曲线.
(Ⅱ) .
.
【解析】
试题分析:(I)设动点为M,其坐标为 ,
,
当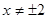 时,由条件可得
时,由条件可得 ,
,
即 ,又
,又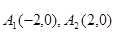 的坐标满足
的坐标满足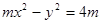 ,故依题意,曲线
,故依题意,曲线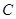 的方程为
的方程为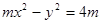 .
.
当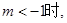 曲线
曲线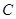 的方程为
的方程为 ,
,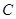 是焦点在
是焦点在 轴上的椭圆;
轴上的椭圆;
当 时,曲线
时,曲线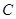 的方程为
的方程为 ,
,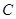 是圆心在原点,半径为2的圆;
是圆心在原点,半径为2的圆;
当 时,曲线
时,曲线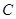 的方程为
的方程为 ,
,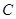 是焦点在
是焦点在 轴上的椭圆;
轴上的椭圆;
当 时,曲线
时,曲线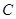 的方程为
的方程为 ,
,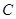 是焦点在
是焦点在 轴上的双曲线.
轴上的双曲线.
(Ⅱ)曲线 ;
; ,
,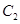 :
: , 设圆
, 设圆 的斜率为
的斜率为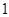 的切线
的切线 和椭圆
和椭圆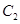 交于A(x1,y1),B(x2,y2)两点,令直线AB的方程为
交于A(x1,y1),B(x2,y2)两点,令直线AB的方程为 ,①
,①
将其代入椭圆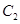 的方程并整理得
的方程并整理得
由韦达定理得 ②
②
因为 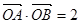 ,所以
,所以  ③
③
将①代入③并整理得 
联立②得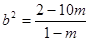 ④,因为直线AB和圆
④,因为直线AB和圆 相切,因此
相切,因此 ,
, ,
,
由④得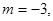 所以曲线
所以曲线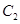 的方程
的方程 ,即
,即 .
.
考点:直线与圆锥曲线的综合问题;圆锥曲线的轨迹问题.
点评:本题考查直线与圆锥曲线的综合问题,着重考查圆锥曲线的轨迹问题,突出化归思想、分类讨论思想、方程思想的考查,综合性强,难度大,属于难题.


科目:高中数学 来源:2011-2012学年宁夏高三第六次月考理科数学试卷 题型:解答题
平面内与两定点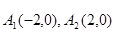 连线的斜率之积等于非零常数
连线的斜率之积等于非零常数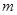 的点的轨迹,加上
的点的轨迹,加上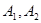 两点,所成的曲线
两点,所成的曲线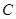 可以是圆,椭圆或双曲线.
可以是圆,椭圆或双曲线.
(I)求曲线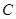 的方程,并讨论
的方程,并讨论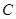 的形状与
的形状与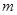 值的关系.
值的关系.
(Ⅱ)当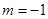 时,对应的曲线为
时,对应的曲线为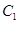 ;对给定的
;对给定的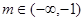 ,对应的曲线为
,对应的曲线为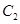 ,若曲线
,若曲线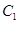 的斜率为
的斜率为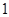 的切线与曲线
的切线与曲线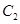 相交于
相交于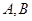 两点,且
两点,且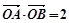 (
(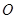 为坐标原点),求曲线
为坐标原点),求曲线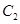 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
平面内与两定点![]() 连线的斜率之积等于非零常数
连线的斜率之积等于非零常数![]() 的点的轨迹,加上
的点的轨迹,加上![]() 两点,所成的曲线
两点,所成的曲线![]() 可以是圆,椭圆或双曲线.
可以是圆,椭圆或双曲线.
(Ⅰ)求曲线![]() 的方程,并讨论
的方程,并讨论![]() 的形状与
的形状与![]() 值的关系;
值的关系;
(Ⅱ)当![]() 时,对应的曲线为
时,对应的曲线为![]() ;对给定的
;对给定的![]() ,对应的曲线为
,对应的曲线为![]() ,若曲线
,若曲线![]() 的斜率为
的斜率为![]() 的切线与曲线
的切线与曲线![]() 相交于
相交于![]() 两点,且
两点,且![]() (
(![]() 为坐标原点),求曲线
为坐标原点),求曲线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
平面内与两定点![]() 连线的斜率之积等于常数
连线的斜率之积等于常数![]() (
(![]() 的点的轨迹,连同
的点的轨迹,连同![]() 两点所成的曲线为C.
两点所成的曲线为C.
(Ⅰ)求曲线C的方程,并讨论C的形状;
(II)设![]() ,
,![]() ,对应的曲线是
,对应的曲线是![]() ,已知动直线
,已知动直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两不同点,且
两不同点,且![]() ,其中O为坐标原点,探究
,其中O为坐标原点,探究 ![]() 是否为定值,写出解答过程。
是否为定值,写出解答过程。
查看答案和解析>>
科目:高中数学 来源:宁夏银川一中2011-2012学年高三第六次月考试题(数学理) 题型:解答题
平面内与两定点 连线的斜率之积等于非零常数
连线的斜率之积等于非零常数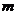 的点的轨迹,加上
的点的轨迹,加上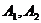 两点,所成的曲线
两点,所成的曲线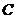 可以是圆,椭圆或双曲线.
可以是圆,椭圆或双曲线.
(I)求曲线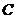 的方程,并讨论
的方程,并讨论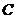 的形状与
的形状与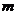 值的关系.
值的关系.
(Ⅱ)当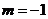 时,对应的曲线为
时,对应的曲线为 ;对给定的
;对给定的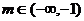 ,对应的曲线为
,对应的曲线为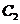 ,若曲线
,若曲线 的斜率为
的斜率为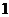 的切线与曲线
的切线与曲线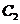 相交于
相交于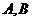 两点,且
两点,且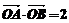 (
( 为坐标原点),求曲线
为坐标原点),求曲线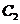 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com