
分析 (1)由已知中函数的解析式,求出导函数的解析式,对k进行分类讨论,确定x在不同情况下导函数的符号,进而可得函数的单调性.
(2)根据(1)中函数的单调性k>0时,讨论k取不同值时函数零点个数,最后综合讨论结果,可得答案.
解答 解:(1)由f(x)=ex-kx,x∈R,得f'(x)=ex-k,
①当k≤0时,则f'(x)=ex-k>0对x∈R恒成立,
此时f(x)的单调递增,递增区间为(-∞,+∞);
②当k>0时,
由f'(x)=ex-k>0,得到x>lnk,
由f'(x)=ex-k<0,得到x<lnk,
所以,k>0时,f(x)的单调递增区间是(lnk,+∞);递减区间是(-∞,lnk);
综上,当k≤0时,f(x)的单调递增区间为(-∞,+∞).
(2)当k>0时,f(x)的单调递增区间是(lnk,+∞);递减区间是(-∞,lnk),
当k>0时,令f'(x)=ex-k=0,
得x=lnk,且f(x)在(-∞,lnk)上单调递减,在(lnk,+∞)上单调递增,f(x)在x=lnk时取得极小值,
即f(x)在(-∞,4]上最多存在两个零点.
(ⅰ)若函数f(x)在(-∞,4]上有2个零点,
则 $\left\{\begin{array}{l}{lnk<4}\\{f(lnk)=k(1-lnk)<0}\\{f(4)≥0}\end{array}\right.$,
解得k∈(e,$\frac{{e}^{4}}{4}$];
(ⅱ)若函数f(x)在(-∞,4]上有1个零点,
则f(4)<0或 $\left\{\begin{array}{l}{lnk≤4}\\{f(lnk)=0}\end{array}\right.$,
解得k∈($\frac{{e}^{4}}{4}$,+∞)或k=e;
(ⅲ)若函数f(x)在(-∞,4]上没有零点,
则 $\left\{\begin{array}{l}{lnk>4}\\{f(4)>0}\end{array}\right.$或f(lnk)=k(1-lnk)>0,
解得k∈(0,e).
综上所述,当k∈(e,$\frac{{e}^{4}}{4}$]时,f(x)在(-∞,4]上有2个零点;
当k∈($\frac{{e}^{4}}{4}$,+∞)∪(-∞,0)或k=e时,f(x)在(-∞,4]上有1个零点;
当k∈[0,e)时,f(x)在(-∞,4]上无零点.
点评 本题考查的知识点是根的存在性及根的个数判断,利用导数研究函数的单调性,是导数的综合应用,特别是第(2)中分类比较复杂,难度较大.


科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{5}}{3}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | -$\frac{2}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
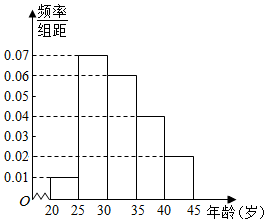 为了增强市民的环境保护组织,某市面向全市征召n名义务宣传志愿者,成立环境保护宣传组织,现按年龄把该组织的成员分成5组:[20,25),[25,30),[30,35),[35,40),[40,45]. 得到的频率分布直方图如图所示,已知该组织的成员年龄在[35,40)内有20人
为了增强市民的环境保护组织,某市面向全市征召n名义务宣传志愿者,成立环境保护宣传组织,现按年龄把该组织的成员分成5组:[20,25),[25,30),[30,35),[35,40),[40,45]. 得到的频率分布直方图如图所示,已知该组织的成员年龄在[35,40)内有20人查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图已知四棱锥P-ABCD的底面ABCD是边长为2的正方形,PD⊥底面ABCD,E,F分别为棱BC、AD的中点
如图已知四棱锥P-ABCD的底面ABCD是边长为2的正方形,PD⊥底面ABCD,E,F分别为棱BC、AD的中点查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 函数f(x)=Acos(ωx+φ)(A,ω,φ为常数,A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{π}{6}$)等于( )
函数f(x)=Acos(ωx+φ)(A,ω,φ为常数,A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{π}{6}$)等于( )| A. | $\frac{\sqrt{6}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某几何体的三视图如下,则几何体的表面积为( )
某几何体的三视图如下,则几何体的表面积为( )| A. | 2$\sqrt{5}$+2$\sqrt{2}$ | B. | 6+2$\sqrt{3}$+2$\sqrt{2}$ | C. | 2+2$\sqrt{5}$+2$\sqrt{2}$ | D. | 6+2$\sqrt{5}$+2$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com