
【题目】已知函数 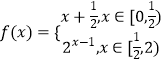 ,若存在x1 , x2 , 当0≤x1<x2<2时,f(x1)=f(x2),则x1f(x2)﹣f(x2)的取值范围为( )
,若存在x1 , x2 , 当0≤x1<x2<2时,f(x1)=f(x2),则x1f(x2)﹣f(x2)的取值范围为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:作出函数的图象:
∵存在x1 , x2 , 当0≤x1<x2<2时,f(x1)=f(x2)
∴0≤x1< ![]() ,
,
∵x+ ![]() 在[0,
在[0, ![]() )上的最小值为
)上的最小值为 ![]() ;
;
2x﹣1在[ ![]() ,2)的最小值为
,2)的最小值为 ![]() ,
,
∴x1+ ![]() ≥
≥ ![]() ,x1≥
,x1≥ ![]() ,
,
∴ ![]() ≤x1<
≤x1< ![]() .
.
∵f(x1)=x1+ ![]() ,f(x1)=f(x2)
,f(x1)=f(x2)
∴x1f(x2)﹣f(x2)=x1f(x1)﹣f(x1)2
= ![]() ﹣(x1+
﹣(x1+ ![]() )=x12﹣
)=x12﹣ ![]() x1﹣
x1﹣ ![]() ,
,
设y=x12﹣ ![]() x1﹣
x1﹣ ![]() =(x1﹣
=(x1﹣ ![]() )2﹣
)2﹣ ![]() ,(
,( ![]() ≤x1<
≤x1< ![]() ),
),
则对应抛物线的对称轴为x= ![]() ,
,
∴当x= ![]() 时,y=﹣
时,y=﹣ ![]() ,
,
当x= ![]() 时,y=
时,y= ![]() ,
,
即x1f(x2)﹣f(x2)的取值范围为[﹣ ![]() ,
, ![]() ).
).
故选:B.
先作出函数图象然后根据图象,根据f(x1)=f(x2),确定x1的取值范围然后再根据x1f(x2)﹣f(x2),转化为求在x1的取值范围即可.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)是(﹣∞,0)∪(0,+∞)上的偶函数,x>0时f(x)=x﹣ ![]() ,求x<0时f(x)的表达式,判断f(x)在(﹣∞,0)上的单调性,并用定义给出证明.
,求x<0时f(x)的表达式,判断f(x)在(﹣∞,0)上的单调性,并用定义给出证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着我国经济的迅速发展,居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
时间代号x | 1 | 2 | 3 | 4 | 5 |
储蓄存款y (千亿元) | 5 | 6 | 7 | 8 | 10 |
附:回归方程 ![]() 中,
中, ![]() =
=  .
.
(1)求y关于x的线性回归方程 ![]() ;
;
(2)用所求回归方程预测该地区今年的人民币储蓄存款.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设y1=loga(3x+1),y2=loga(﹣3x),其中a>0且a≠1.
(1)若y1=y2 , 求x的值;
(2)若y1>y2 , 求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于0<a<1,给出下列四个不等式( )
①loga(1+a)<loga(1+ ![]() );
);
②loga(1+a)<loga(1+ ![]() );
);
③a1+a<a ![]() ;
;
④a1+a<a ![]() ;
;
其中成立的是( )
A.①③
B.①④
C.②③
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是圆O的直径,PB是圆O的切线,过A点作AE∥OP交圆O于E点,PA交圆O于点F,连接PE. 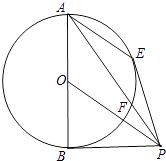
(1)求证:PE是圆O的切线;
(2)设AO=3,PB=4,求PF的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3﹣3x
(1)求函数f(x)的单调区间,并求函数f(x)的极值;
(2)若方程x3﹣3x﹣a+1=0有三个相异的实数根,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四种说法:
①函数y=ax(a>0且a≠1)与函数y=logaax(a>0且a≠1)的定义域相同;
②函数y=x3与y=3x的值域相同;
③函数y= ![]() +
+ ![]() 与y=
与y= ![]() 都是奇函数;
都是奇函数;
④函数y=(x﹣1)2与y=2x﹣1在区间[0,+∞)上都是增函数.
其中正确的序号是(把你认为正确叙述的序号都填上).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com