
【题目】设函数![]() (
(![]() ).
).
(1)若函数![]() 在定义域上是单调函数,求实数
在定义域上是单调函数,求实数![]() 的取值范围;
的取值范围;
(2)求函数![]() 的极值点;
的极值点;
(3)令![]() ,
, ![]() ,设
,设![]() ,
, ![]() ,
, ![]() 是曲线
是曲线![]() 上相异三点,其中
上相异三点,其中![]() .求证:
.求证: ![]() .
.
【答案】(1)实数![]() 的取值范围是
的取值范围是![]()
(2)![]() 时,
时, ![]() 有唯一极小值点
有唯一极小值点![]() ,
,
![]() 时,
时, ![]() 有一个极大值点
有一个极大值点![]() 和一个极小值点
和一个极小值点![]() ;
;
![]() 时,
时, ![]() 无极值点.
无极值点.
(3)证明见解析
【解析】试题分析:(1)利用导数转化为: ![]() 或
或![]() 在
在![]() 上恒成立.再根据变量分离转化为对应函数最值:
上恒成立.再根据变量分离转化为对应函数最值: ![]() 最大值或
最大值或![]() 最小值,即得
最小值,即得![]() .(2)实质为讨论一元二次方程
.(2)实质为讨论一元二次方程![]() 解的情况:当
解的情况:当![]() 时,方程无解,函数无极值点;
时,方程无解,函数无极值点; ![]() 时,方程有一解,函数有一个极值点;
时,方程有一解,函数有一个极值点; ![]() 时,方程有两解,函数有两个极值点;(3)借助第三量
时,方程有两解,函数有两个极值点;(3)借助第三量![]() 进行论证,先证
进行论证,先证![]() ,代入化简可得
,代入化简可得![]() ,构造函数
,构造函数![]() ,其中
,其中![]() (
(![]() ),利用导数易得
),利用导数易得![]() 在
在![]() 上单调递增,即
上单调递增,即![]() ,即有
,即有![]() ,同理可证
,同理可证![]() ,
,
试题解析:解:(1) ,
,
![]() 函数
函数![]() 在定义域上是单调函数,
在定义域上是单调函数, ![]() 或
或![]() 在
在![]() 上恒成立.
上恒成立.
若![]() 恒成立,得
恒成立,得![]() .
.
若![]() 恒成立,即
恒成立,即![]() 恒成立.
恒成立.
![]() 在
在![]() 上没有最小值,
上没有最小值, ![]() 不存在实数
不存在实数![]() 使
使![]() 恒成立.
恒成立.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.
(2)由(1)知当![]() 时,函数
时,函数![]() 无极值点.
无极值点.
当![]() 时,
时, ![]() 有两个不同解,
有两个不同解, ![]() ,
, ![]() ,
,
![]() 时,
时, ![]() ,
, ![]() ,即
,即![]() ,
, ![]() ,
,
![]() 时,
时, ![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,
上递增, ![]() 有唯一极小值点
有唯一极小值点![]() ;
;
当![]() 时,
时, ![]() .
.
![]() ,
, ![]() ,
, ![]() 在
在![]() 上递增,在
上递增,在![]() 递减,在
递减,在![]() 递增,
递增,
![]() 有一个极大值点
有一个极大值点![]() 和一个极小值点
和一个极小值点![]() .
.
综上所述, ![]() 时,
时, ![]() 有唯一极小值点
有唯一极小值点![]() ,
,
![]() 时,
时, ![]() 有一个极大值点
有一个极大值点![]() 和一个极小值点
和一个极小值点![]() ;
;
![]() 时,
时, ![]() 无极值点.
无极值点.
(3)先证: ![]() ,即证
,即证![]() ,
,
即证![]()
![]() ,
,
令![]() (
(![]() ),
),![]() ,
, ![]() ,
,
所以![]() 在
在![]() 上单调递增,即
上单调递增,即![]() ,即有
,即有![]() ,所以获证.
,所以获证.
同理可证: ![]() ,
,
所以![]() .
.


科目:高中数学 来源: 题型:
【题目】2015年年岁史诗大剧《芈月传》风靡大江南北,影响力不亚于以前的《甄嬛传》,某记者调查了大量《芈月传》的观众,发现年龄段与爱看的比例存在较好的线性相关关系,年龄在![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 的爱看比例分别为
的爱看比例分别为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,现用这5个年龄段的中间值
,现用这5个年龄段的中间值![]() 代表年龄段,如12代表
代表年龄段,如12代表![]() ,17代表
,17代表![]() ,根据前四个数据求得
,根据前四个数据求得![]() 关于爱看比例
关于爱看比例![]() 的线性回归方程为
的线性回归方程为![]() ,由此可推测
,由此可推测![]() 的值为( )
的值为( )
A. 33 B. 35 C. 37 D. 39
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱(侧棱与底面垂直的棱柱)ABC﹣A1B1C1中,点G是AC的中点.

(1)求证:B1C∥平面 A1BG;
(2)若AB=BC, ![]() ,求证:AC1⊥A1B.
,求证:AC1⊥A1B.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一支车队有![]() 辆车,某天依次出发执行运输任务。第一辆车于下午
辆车,某天依次出发执行运输任务。第一辆车于下午![]() 时出发,第二辆车于下午
时出发,第二辆车于下午![]() 时
时![]() 分出发,第三辆车于下午
分出发,第三辆车于下午![]() 时
时![]() 分出发,以此类推。假设所有的司机都连续开车,并都在下午
分出发,以此类推。假设所有的司机都连续开车,并都在下午![]() 时停下来休息.
时停下来休息.
到下午![]() 时,最后一辆车行驶了多长时间?
时,最后一辆车行驶了多长时间?
如果每辆车的行驶速度都是![]() ,这个车队当天一共行驶了多少
,这个车队当天一共行驶了多少![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,已知在菱形![]() 中,
中, ![]() ,
, ![]() 为
为![]() 的中点,现将四边形
的中点,现将四边形![]() 沿
沿![]() 折起至
折起至![]() ,如图2.
,如图2.

(1)求证: ![]() 面
面![]() ;
;
(2)若二面角![]() 的大小为
的大小为![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)的定义域为R,当x<0时,f(x)>1,且对任意的实数x,y∈R,等式f(x)f(y)=f(x+y)成立,若数列{an}满足 ![]() ,(n∈N*),且a1=f(0),则下列结论成立的是( )
,(n∈N*),且a1=f(0),则下列结论成立的是( )
A.f(a2013)>f(a2016)
B.f(a2014)>f(a2015)
C.f(a2016)<f(a2015)
D.f(a2014)<f(a2016)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,以原点O为圆心,椭圆的短半轴长为半径的圆与直线x﹣y+
,以原点O为圆心,椭圆的短半轴长为半径的圆与直线x﹣y+![]() =0相切.
=0相切.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线l:y=kx+m与椭圆C相交于A、B两点,且kOAkOB=﹣![]() ,判断△AOB的面积是否为定值?若为定值,求出定值;若不为定值,说明理由.
,判断△AOB的面积是否为定值?若为定值,求出定值;若不为定值,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,周长为7.5cm,且sinA:sinB:sinC=4:5:6,下列结论:
①a:b:c=4:5:6 ②a:b:c=2: ![]() ③a=2cm,b=2.5cm,c=3cm ④A:B:C=4:5:6
③a=2cm,b=2.5cm,c=3cm ④A:B:C=4:5:6
其中成立的个数是( )
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据国家环保部新修订的《环境空气质量标准》规定:居民区![]() 的年平均浓度不得超过35微克/立方米,
的年平均浓度不得超过35微克/立方米, ![]() 的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年30天
的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年30天![]() 的24小时平均浓度(单位:微克/立方米)的监测数据,将这30天的测量结果绘制成样本频率分布直方图如图.
的24小时平均浓度(单位:微克/立方米)的监测数据,将这30天的测量结果绘制成样本频率分布直方图如图.
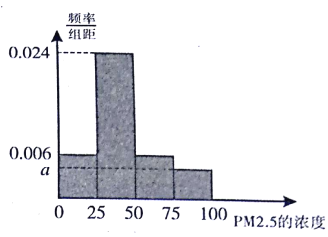
(Ⅰ)求图中![]() 的值;
的值;
(Ⅱ)由频率分布直方图中估算样本平均数,并根据样本估计总体的思想,从![]() 的年平均浓度考虑,判断该居民区的环境质量是否需要改善?并说明理由.
的年平均浓度考虑,判断该居民区的环境质量是否需要改善?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com