
【题目】国家为了鼓励节约用水,实行阶梯用水收费制度,价格参照表如表:
用水量(吨) | 单价(元/吨) | 注 |
0~20(含) | 2.5 | |
20~35(含) | 3 | 超过20吨不超过35吨的部分按3元/吨收费 |
35以上 | 4 | 超过35吨的部分按4元/吨收费 |
(1)若小明家10月份用水量为30吨,则应缴多少水费?
(2)若小明家10月份缴水费99元,则小明家10月份用水多少吨?
(3)写出水费y与用水量x之间的函数关系式,并画出函数的图象.
【答案】
(1)解: 20×2.5+(30﹣20)×3=80
(2)解:第一档最多为50元
第二档最多为50+(35﹣20)×3元=95元
∴用水量在第三档内,99﹣95=4,4÷4=1
∴用水量为35+1=36吨.
(3)解:0<x≤20时,f(x)=2.5x;
20<x≤35时,f(x)=20×2.5+(x﹣20)×3=3x﹣10;
x>35时,f(x)=20×2.5+(35﹣20)×3+(x﹣35)×4=4x﹣45;
∴f(x)=  .
.
函数的图象如图所示.
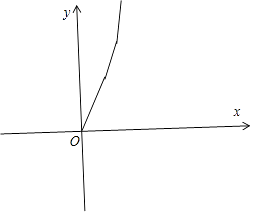
【解析】(1)小明家10月份用水量为30吨,在第二档,可得结论;(2)第一档最多为50元,二档最多为50+(35﹣20)×3元=95元,可得用水量在第三档内,即可得出结论;(3)利用所给条件,即可写出水费y与用水量x之间的函数关系式,并画出函数的图象.


科目:高中数学 来源: 题型:
【题目】如图所示,在棱长为2cm的正方体ABCD﹣A1B1C1D1中,A1B1的中点是P,过点A1作出与截面PBC1平行的截面,简单证明截面形状,并求该截面的面积.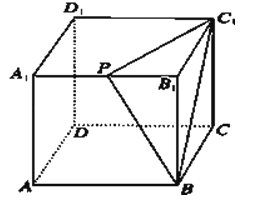
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设M={x|0≤x≤2},N={y|0≤y≤2},给出下列四个图形: 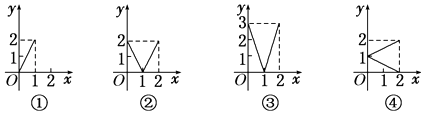
其中,能表示从集合M到集合N的函数关系的个数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣ax﹣2a2(x∈R).
(1)关于x的不等式f(x)<0的解集为A,且A[﹣1,2],求a的取值范围;
(2)是否存在实数a,使得当x∈R时, ![]() 成立.若存在给出证明,若不存在说明理由.
成立.若存在给出证明,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位附近只有甲、乙两个临时停车场,它们各有![]() 个车位,为了方便市民停车,某互联网停车公司对这两个停车场,在某些固定时刻的剩余停车位进行记录,如下表:
个车位,为了方便市民停车,某互联网停车公司对这两个停车场,在某些固定时刻的剩余停车位进行记录,如下表:
时间 停车场 |
|
|
|
|
|
|
甲停车场 |
|
|
|
|
|
|
乙停车场 |
|
|
|
|
|
|
如果表中某一时刻剩余停车位数低于该停车场总车位数的![]() ,那么当车主驱车抵达单位附近时,该公司将会向车主发出停车场饱和警报.
,那么当车主驱车抵达单位附近时,该公司将会向车主发出停车场饱和警报.
(1)假设某车主在以上六个时刻抵达单位附近的可能性相同,求他收到甲停车场饱和警报的概率;
(2)从这六个时刻中任选一个时刻,求甲停车场比乙停车场剩余车位数少的概率;
(3)当乙停车场发出饱和警报时,求甲停车场也发出饱和警报的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
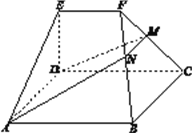
【题目】如图,在几何体![]() 中,底面
中,底面![]() 为矩形,
为矩形, ![]() ,
, ![]() .点
.点![]() 在棱
在棱![]() 上,平面
上,平面![]() 与棱
与棱![]() 交于点
交于点![]() .
.
(Ⅰ)求证: ![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)若![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,求二面角
,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(Ⅰ)抛物线的顶点在原点,坐标轴为对称轴,并经过点![]() ,求此抛物线的方程.
,求此抛物线的方程.
(Ⅱ)已知圆: ![]() (
(![]() ),把圆上的各点纵坐标不变,横坐标伸长到原来的
),把圆上的各点纵坐标不变,横坐标伸长到原来的![]() 倍得一椭圆.求椭圆方程,并证明椭圆离心率是与
倍得一椭圆.求椭圆方程,并证明椭圆离心率是与![]() 无关的常数.
无关的常数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com