
【题目】设 A 、B 、Ai ![]() 为集合.
为集合.
(1)满足 A ∪ B ={a , b}的集合有序对(A , B)有多少对 ? 为什么 ?
(2)满足 A ∪ B ={a1 , a2 , …, ![]() }的集合有序对(A , B)有多少对? 为什么?
}的集合有序对(A , B)有多少对? 为什么?
(3)满足![]() 的集合有序组
的集合有序组![]() 有多少组? 为什么 ?
有多少组? 为什么 ?
【答案】(1)9 (2)![]() (3)
(3)![]()
【解析】
(1)9 (2)![]() (3)
(3)![]() (1)、(2)都是(3)的特例, 故只证(3).
(1)、(2)都是(3)的特例, 故只证(3).
确定集合有序组![]() 的组数可分 n步.
的组数可分 n步.
第一步考虑 ![]() 属于
属于![]() 的可能, 对
的可能, 对![]() 有
有![]() 、
、![]() 两种可能, 对
两种可能, 对![]() 也有两种可能…, 对
也有两种可能…, 对 ![]() 来说也有两种可能,这样共有 2k 种可能.
来说也有两种可能,这样共有 2k 种可能.
但因A1 ∪ A 2∪ … ∪ ![]() ={a1 , a2 , … , an},所以应排除
={a1 , a2 , … , an},所以应排除![]() 、
、![]() ,…,
,…,![]() 的可能, 故有2k-1 种可能.
的可能, 故有2k-1 种可能.
同理, 第二步考虑 a2 属于 A1, A 2, …, Ak 的可能, 也有 2k -1 种可能. ……
第 n 步考虑an 属于 A1 , A 2 , …, Ak 的可能, 也有2k -1 种可能.
由乘法原理, 得(A 1 , A2 , …, Ak)的组数是(2k -1)n .


科目:高中数学 来源: 题型:
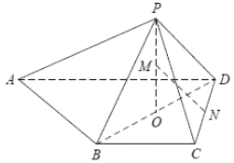
【题目】已知四棱锥![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 在底面
在底面![]() 上的射影是
上的射影是![]() 的中点
的中点![]() ,
,![]() .
.
(1)求证:直线![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,求直线
的中点,求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)当四棱锥![]() 的体积最大时,求二面角
的体积最大时,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家质量监督检验检疫局于2004年5月31日发布了新的《车辆驾驶人员血液、呼气酒精含量阈值与检验》国家标准,新标准规定,车辆驾驶人血液中的酒精含量大于或等于20毫克/百毫升、小于80毫克/百毫升的行为饮酒驾车,血液中的酒精含量大于或等于80毫克/百毫升为醉酒驾车,经过反复试验,喝一瓶啤酒后酒精在人体血液内的变化规律“散点图”如下:

该函数模型如下,
 .
.
根据上述条件,回答以下问题:
(1)试计算喝1瓶啤酒后多少小时血液中的酒精含量达到最大值?最大值是多少?
(2)试计算喝1瓶啤酒后多少小时才可以驾车?(时间以整小时计)(参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1:y=cos x,C2:y=sin (2x+![]() ),则下面结论正确的是( )
),则下面结论正确的是( )
A. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
B. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
C. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
D. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国庆期间,某旅行社组团去风景区旅游,若旅行团人数在30人或30人以下,每人需交费用为900元;若旅行团人数多于30人,则给予优惠:每多1人,人均费用减少10元,直到达到规定人数75人为止.旅行社需支付各种费用共计15000元.
(1)写出每人需交费用![]() 关于人数
关于人数![]() 的函数;
的函数;
(2)旅行团人数为多少时,旅行社可获得最大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了缓解市民吃肉难的生活问题,某生猪养殖公司欲将一批猪肉用冷藏汽车从甲地运往相距![]() 千米的乙地,运费为每小时
千米的乙地,运费为每小时![]() 元,装卸费为
元,装卸费为![]() 元,猪肉在运输途中的损耗费(单位:元)是汽车速
元,猪肉在运输途中的损耗费(单位:元)是汽车速![]() 度值的
度值的![]() 倍.(说明:运输的总费用=运费+装卸费+损耗费)
倍.(说明:运输的总费用=运费+装卸费+损耗费)
(1)若汽车的速度为每小时![]() 千米,试求运输的总费用;
千米,试求运输的总费用;
(2)为使运输的总费用不超过![]() 元,求汽车行驶速度的范围;
元,求汽车行驶速度的范围;
(3)若要使运输的总费用最小,汽车应以每小时多少千米的速度行驶?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为丰富市民的文化生活,市政府计划在一块半径为100m的扇形土地OAB上建造市民广场.规划设计如图:矩形EFGH(其中E,F在圆弧AB上,G,H在弦AB上)区域为运动休闲区,△OAB区域为文化展示区,其余空地为绿化区域,已知P为圆弧AB中点,OP交AB于M,cos∠POB=![]() ,记矩形EFGH区域的面积为Sm2.
,记矩形EFGH区域的面积为Sm2.

(1)设∠POF=θ(rad),将S表示成θ的函数;
(2)求矩形EFGH区域的面积S的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com