
(1)若PA=PB=PC,则O为△ABC的 心;
(2)若PA⊥PB,PB⊥PC,PC⊥PA,则O为△ABC的? ?心;
(3)P到三边AB、BC、CA的距离相等,则O为△ABC的? ?心;
(4)若PA=PB=PC,∠C=90°,则O是AB边的 点;
(5)若PA=PB=PC,AB=AC,则O点在 线上.
解析:(1)如图,∵PO⊥α,PA=PB=PC,由射影定理不难得到OA=OB=OC,即O是外心.?
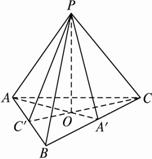
(2)如图,由条件PA、PB、PC两两垂直可得AP⊥面PBC![]() PA⊥BC
PA⊥BC![]() BC⊥
BC⊥![]() AA′,同理可得AB⊥CC′,由此可知O为垂心.?
AA′,同理可得AB⊥CC′,由此可知O为垂心.?
(3)如图,若PA′⊥BC,PC′⊥AB?CO⊥AB,AO⊥BC.?
又PA′=PC′![]() OC′=OA′,可知O为内心.?
OC′=OA′,可知O为内心.?
(4)由(1)知O为△ABC的外心,而△ABC为直角三角形,故O为AB的中点.?
(5)由(1)知O为△ABC的外心,而AB=AC,故O在△ABC的边BC的中线上(或高或∠BAC的平分线).
答案:(1)外 (2)垂 (3)内 (4)中 (5)中


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2014届浙江省高二9月质量检测文科数学试卷(解析版) 题型:填空题
过△ABC所在平面a外一点P,作OP⊥a,垂足为O,连接PA,PB,PC,
若PA=PB=PC,则点O为△ABC的 心。
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com