练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在三棱锥中，平面平面，，，若为的中点.

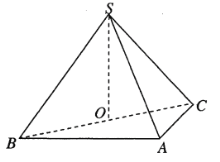
    （1）证明：平面；

    （2）求异面直线和所成角；

    （3）设线段上有一点，当与平面所成角的正弦值为时，求的长.

    【答案】(1)证明见解析；(2)(3).

    【解析】

    （1）先证明平面平面，再证明平面；（2）分别以，，为轴，轴，轴的非负半轴，建立空间直角坐标系，利用向量法求异面直线和所成角；（3）设，，利用向量法得到，解方程即得t的值和的长.

    （1）∵，，

    ∴，

    ∵平面平面，

    平面平面，

    平面，

    ∴平面.

    （2）∵，，

    ∴，，

    如图，分别以，，为轴，轴，轴的非负半轴，建立空间直角坐标系,

    ∵，，，，

    ∴，，

    ∵，

    ∴异面直线和所成角为.

    （3）设为平面的法向量，

    ∵，，

    ∴，即，

    设，，

    ∴，

    设与平面所成角为，

    ∵，

    ∴，

    ，

    ，

    ，

    （舍），，

    ∴的长为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设函数，（为常数），．曲线在点处的切线与轴平行

    （1）求的值；

    （2）求的单调区间和最小值；

    （3）若对任意恒成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某快递公司收取快递费用的标准是：重量不超过的包裹收费10元；重量超过的包裹，除收费10元之外，超过的部分，每超出（不足，按计算）需再收5元.

    该公司对近60天，每天揽件数量统计如下表：

    （1）某人打算将三件礼物随机分成两个包裹寄出，求该人支付的快递费不超过30元的概率；

    （2）该公司从收取的每件快递的费用中抽取5元作为前台工作人员的工资和公司利润，剩余的作为其他费用.前台工作人员每人每天揽件不超过150件，工资100元，目前前台有工作人员3人，那么，公司将前台工作人员裁员1人对提高公司利润是否更有利？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】随着节能减排意识深入人心以及共享单车在饶城的大范围推广，越来越多的市民在出行时喜欢选择骑行共享单车。为了研究广大市民在共享单车上的使用情况，某公司在我市随机抽取了100名用户进行调查，得到如下数据：

    每周使用次数

    1次

    2次

    3次

    4次

    5次

    6次及以上

    男

    4

    3

    3

    7

    8

    30

    女

    6

    5

    4

    4

    6

    20

    合计

    10

    8

    7

    11

    14

    50

    （1）如果认为每周使用超过3次的用户为“喜欢骑行共享单车”，请完成列表（见答题卡），并判断能否在犯错误概率不超过0.05的前提下，认为是否“喜欢骑行共享单车”与性别有关？

    （2）每周骑行共享单车6次及6次以上的用户称为“骑行达人”，视频率为概率，在我市所有“骑行达人”中，随机抽取4名用户.

    ① 求抽取的4名用户中，既有男生“骑行达人”又有女“骑行达人”的概率；

    ②为了鼓励女性用户使用共享单车，对抽出的女“骑行达人”每人奖励500元，记奖励总金额为，求的分布列及数学期望．

    附表及公式：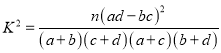

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线的顶点在坐标原点，过抛物线的焦点的直线与该抛物线交于两点， 面积的最小值为2．

    （1）求抛物线的标准方程；

    （2）试问是否存在定点，过点的直线与抛物线交于两点，当三点不共线时，使得以为直径的圆必过点．若存在，求出所有符合条件的点；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知ω＞0，0＜φ＜π，直线和是函数f（x）＝sin（ωx+φ）图象的两条相邻的对称轴，若将函数f（x）图象上每一点的横坐标变为原来的倍，纵坐标变为原来的2倍，则得到的图象的函数解析式是（ ）

    A.B.

    C.y＝2cos2xD.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线C的顶点在坐标原点，焦点F在x轴上，抛物线C上一点到焦点F的距离为．

    Ⅰ求抛物线C的标准方程；

    Ⅱ设点，过点的直线l与抛物线C相交于A，B两点，记直线MA与直线MB的斜率分别为，，证明：为定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校为了解高二年级学生某次数学考试成绩的分布情况，从该年级的1120名学生中随机抽取了100名学生的数学成绩，发现都在内现将这100名学生的成绩按照，，，，，，分组后，得到的频率分布直方图如图所示,则下列说法正确的是　　

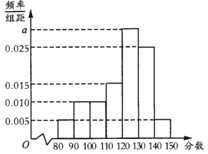
    A. 频率分布直方图中a的值为

    B. 样本数据低于130分的频率为

    C. 总体的中位数保留1位小数估计为分

    D. 总体分布在的频数一定与总体分布在的频数相等

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知四棱锥， 平面，底面中， ， ，且， 为的中点．

    （1）求证：平面平面；

    （2）问在棱上是否存在点，使平面，若存在，请求出二面角的余弦值；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案