分析:方法一(Ⅰ)连结A1D,证明△A1MD1∽△D1A1D,通过计算确定点M的位置;
(Ⅱ)引A1E⊥B1M于E,连结D1E,则A1E是D1E在平面BA1上的射影,说明∠A1ED1是二面角D1-MB1-B的平面角的补角,通过解三角形求二面角D1-MB1-B的大小.
方法二(Ⅰ)通过建立空间直角坐标系,利用向量的数量积求解点M的位置;
(Ⅱ)求出两个平面的法向量,利用空间向量的数量积求二面角D1-MB1-B的大小.
解答:解:(方法一)
(Ⅰ)连结A
1D,在正四棱柱ABCD-A
1B
1C
1D
1中,侧面ADD
1A
1为矩形,
∵A
1C⊥平面MB
1D
1,
∴A
1C⊥D
1M,
因此A
1C在平面AD
1上的射影A
1D⊥D
1M,
∴△A
1MD
1∽△D
1A
1D,
∴A
1M=
==,因此M是A
1A的中点.…(6分)
(Ⅱ)引A
1E⊥B
1M于E,连结D
1E,则A
1E是
D
1E在平面BA
1上的射影,由三垂线定理可
知D
1E⊥B
1M,
∴∠A
1ED
1是二面角D
1-MB
1-B的平面角的补角,
由(Ⅰ)知,A
1M=
,则
tanA1ED1===,
∴
∠A1ED1=,
∴二面角D
1-MB
1-B等于
.…(12分)
(方法二)
如图,在正四棱住ABCD-A
1B
1C
1D
1中,以A为原点,直线AB为x轴,直线AD为y轴建立空间直角坐标系A-xyz,AB=2,AA
1=2
,则
C(2,2,0),D(0,2,0),A
1(0,0,2
),B
1(2,0,2
),D
1(0,2,2
),
设M(0,0,Z),则
=(0,2,2
-z),
=(2,2,
-2),…(3分)
(Ⅰ)∵A
1C⊥平面MB
1D
1,
∴A
1C⊥D
1M,∴
•=0,
∴
4-2(2-z)=0,
∴
z=,∴
AM=,
因此M是A
1A的中点.…(6分)
(Ⅱ)∵A
1C⊥平面MB
1D
1,
∴
=(2,2,-2)是平面MB
1D
1的一个法向量.
又平面A
1B的一个法向量为
=(0,2,0),…(8分)
∴cos<
,>
=.
∵二面角D
1-MB
1-B是钝二面角.…(11分)
∴二面角D
1-MB
1-B等于
.…(12分)
点评:本题考查空间想象能力以及计算能力,立体几何问题的解法有两种思路,一是几何法,一是向量法,注意解题时合理选择方法,做到简便快捷.

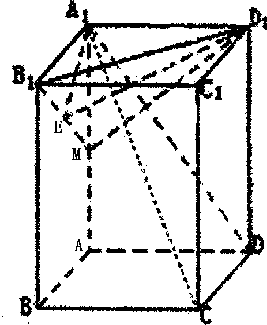
 如图,在正四棱柱ABCD-A1B1C1D1中,已知AB=2,AA1=2
如图,在正四棱柱ABCD-A1B1C1D1中,已知AB=2,AA1=2


 如图,在正四棱柱ABCD-A1B1C1D1中,已知AA1=4,AB=2,E是棱CC1上的一个动点.
如图,在正四棱柱ABCD-A1B1C1D1中,已知AA1=4,AB=2,E是棱CC1上的一个动点. 如图,在正四棱柱ABCD-A′B′C′D′中(底面是正方形的直棱柱),侧棱AA′=
如图,在正四棱柱ABCD-A′B′C′D′中(底面是正方形的直棱柱),侧棱AA′= (2012•青岛一模)如图,在正四棱柱ABCD-A1B1C1D1中,AB=a,AA1=
(2012•青岛一模)如图,在正四棱柱ABCD-A1B1C1D1中,AB=a,AA1= 如图,在正四棱柱ABCD-A1B1C1D1中,AA1=A(x0,y0)AB=2,点E、M分别为A1B、C1C的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,AA1=A(x0,y0)AB=2,点E、M分别为A1B、C1C的中点. (2009•宜昌模拟)如图,在正四棱柱ABCD-A1B1C1D1 中,AB=BC=1,AA1=2.过顶点D1在空间作直线l,使l与直线AC和BC1所成的角都等于60°,这样的直线l最多可作( )
(2009•宜昌模拟)如图,在正四棱柱ABCD-A1B1C1D1 中,AB=BC=1,AA1=2.过顶点D1在空间作直线l,使l与直线AC和BC1所成的角都等于60°,这样的直线l最多可作( )