
【题目】设Sn是数列{an}的前n项和,已知a1=3,an+1=2Sn+3(n∈N)
(I)求数列{an}的通项公式;
(Ⅱ)令bn=(2n﹣1)an , 求数列{bn}的前n项和Tn .
【答案】解:(I)∵an+1=2Sn+3,∴当n≥2时,an=2Sn﹣1+3, ∴an+1﹣an=2(Sn﹣Sn﹣1)=2an , 化为an+1=3an .
∴数列{an}是等比数列,首项为3,公比为3.
∴an=3n .
(II)bn=(2n﹣1)an=(2n﹣1)3n ,
∴数列{bn}的前n项和Tn=3+3×32+5×33+…+(2n﹣1)3n ,
3Tn=32+3×33+…+(2n﹣3)3n+(2n﹣1)3n+1 ,
∴﹣2Tn=3+2(32+33+…+3n)﹣(2n﹣1)3n+1= ![]() ﹣3﹣(2n﹣1)3n+1=(2﹣2n)3n+1﹣6,
﹣3﹣(2n﹣1)3n+1=(2﹣2n)3n+1﹣6,
∴Tn=(n﹣1)3n+1+3
【解析】(I)利用递推关系与等比数列的通项公式即可得出;(II)利用“错位相减法”与等比数列的其前n项和公式即可得出.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:
【题目】已知点P为椭圆 ![]() =1上的动点,EF为圆N:x2+(y﹣1)2=1的任一直径,求
=1上的动点,EF为圆N:x2+(y﹣1)2=1的任一直径,求 ![]() 最大值和最小值是( )
最大值和最小值是( )
A.16,12﹣4 ![]()
B.17,13﹣4 ![]()
C.19,12﹣4 ![]()
D.20,13﹣4 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校100名学生数学竞赛成绩的频率分布直方图如图所示,成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100],则该次数学成绩在[50,60)内的人数为( ) 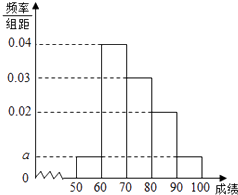
A.20
B.15
C.10
D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,C> ![]() ,若函数y=f(x)在[0,1]上为单调递减函数,则下列命题正确的是( )
,若函数y=f(x)在[0,1]上为单调递减函数,则下列命题正确的是( )
A.f(cosA)>f(cosB)
B.f(sinA)>f(sinB)
C.f(sinA)>f(cosB)
D.f(sinA)<f(cosB)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP= ![]() .
.
(Ⅰ)求证:AB⊥PC;
(Ⅱ)求点D到平面PAC的距离.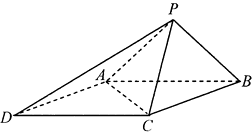
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}的各项均为正数,且a5a6+a4a7=18,则log3a1+log3a2+…+log3a10=( )
A.5
B.9
C.log345
D.10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在以下关于向量的命题中,不正确的是( )
A.若向量 ![]() ,向量
,向量 ![]() (xy≠0),则
(xy≠0),则 ![]()
B.若四边形ABCD为菱形,则 ![]()
C.点G是△ABC的重心,则 ![]()
D.△ABC中, ![]() 和
和 ![]() 的夹角等于A
的夹角等于A
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,AD∥BC,且BC=2AD,AD⊥CD,PB⊥CD,点E在棱PD上,且PE=2ED. 
(1)求证:平面PCD⊥平面PBC;
(2)求证:PB∥平面AEC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(m,cos2x),
=(m,cos2x), ![]() =(sin2x,n),设函数f(x)=
=(sin2x,n),设函数f(x)= ![]()
![]() ,且y=f(x)的图象过点(
,且y=f(x)的图象过点( ![]() ,
, ![]() )和点(
)和点( ![]() ,﹣2).
,﹣2).
(1)求m,n的值;
(2)将y=f(x)的图象向左平移φ(0<φ<π)个单位后得到函数y=g(x)的图象.若y=g(x)的图象上各最高点到点(0,3)的距离的最小值为1,求y=g(x)的单调增区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com