练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】甲、乙两位同学参加诗词大赛，各答3道题，每人答对每道题的概率均为，且各人是否答对每道题互不影响.

    （Ⅰ）用表示甲同学答对题目的个数，求随机变量的分布列和数学期望；

    （Ⅱ）设为事件“甲比乙答对题目数恰好多2”，求事件发生的概率.

    【答案】（I）见解析；（II）.

    【解析】

    （I）确定所有可能的取值，由二项分布概率公式可得每个取值对应的概率，由此得到分布列和数学期望；

    （II）将事件分成“甲答对道，乙答对题道”和“甲答对道，乙答对题道”两种情况，结合（I）中所求概率，根据独立事件概率公式计算可得结果.

    （I）所有可能的取值为

    ；；

    ；.

    的分布列为

    数学期望.

    （II）由题意得：事件“甲比乙答对题目数恰好多”发生

    即：“甲答对道，乙答对题道”和“甲答对道，乙答对题道”两种情况

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某校为了增强学生的记忆力和辨识力，组织了一场类似《最强大脑》的PK赛，两队各由4名选手组成，每局两队各派一名选手PK，比赛四局.除第三局胜者得2分外，其余各局胜者均得1分，每局的负者得0分.假设每局比赛A队选手获胜的概率均为，且各局比赛结果相互独立，比赛结束时A队的得分高于B队的得分的概率为( )

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，为平行四边形ABCD所在平面外一点，M,N分别为AB,PC的中点，平面PAD平面PBC＝.

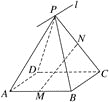
    (1)求证：BC∥；

    (2)MN与平面PAD是否平行？试证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设常数．在平面直角坐标系中，已知点，直线：，曲线：．与轴交于点、与交于点．、分别是曲线与线段上的动点．

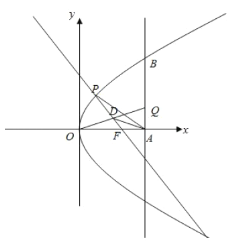
    （1）用表示点到点距离；

    （2）设，，线段的中点在直线，求的面积；

    （3）设，是否存在以、为邻边的矩形，使得点在上？若存在，求点的坐标；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数求：

    （1）的单调区间

    （2）的单调区间在[0,3]上的最大值与最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，矩形所在平面与半圆弧所在平面垂直，是上异于，的点．

    （1）证明：平面平面；

    （2）在线段上是否存在点，使得平面？说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知在直角坐标系xOy中，直线 的参数方程为 （t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为.

    （1）求直线的普通方程和曲线C的直角坐标方程；

    （2）设点P是曲线C上的一个动点，求它到直线的距离d的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若函数在R上是增函数，求实数a的取值范围；

    （2）求所有的实数a，使得对任意时，函数的图象恒在函数图象的下方；

    （3）若存在，使得关于x的方程有三个不相等的实数根，求实数t的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从岳阳到郴州的快速列车包括起始站和终点站共有六站，将这六站分别记为.有一天，张兵和其他18 名旅客乘同一车厢离开岳阳，这些旅客中有些是湖北人，其他的是湖南人，认识所有同车厢旅客的张兵观测到:除了终点站，在每一站，当火车到达时，这节车厢上的湖南人的数目与下车旅客的数目相同，且这次行程中没有新的旅客进入这节车厢.张兵又进一步观测到:当火车离开站时，车厢内有 12名旅客；当火车离开站时，还有 7 名旅客在这一车厢内；当他准备在站下车时，还有5名旅客在这一车厢内.试问开始时火车的这一节车厢有多少湖北人，有多少湖南人？且在旅途中这些数目如何变化？

    查看答案和解析>>

    同步练习册答案