
 ,
, ,
, = .
= .  孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源:2011-2012学年江苏省南通市如东县栟茶高级中学高三(上)第一次学情调研数学试卷(解析版) 题型:解答题
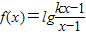 .(k∈R且k>0).
.(k∈R且k>0).查看答案和解析>>
科目:高中数学 来源:2012-2013学年北京市朝阳区高三(上)期中数学试卷(理科)(解析版) 题型:解答题
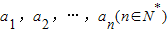 ,任意选取一个实数c,变换T(c)将数列a1,a2,…,an变换为数列|a1-c|,|a2-c|,…,|an-c|,再将得到的数列继续实施这样的变换,这样的变换可以连续进行多次,并且每次所选择的实数c可以不相同,第k(k∈N*)次变换记为Tk(ck),其中ck为第k次变换时选择的实数.如果通过k次变换后,数列中的各项均为0,则称T1(c1),T2(c2),…,Tk(ck)为“k次归零变换”.
,任意选取一个实数c,变换T(c)将数列a1,a2,…,an变换为数列|a1-c|,|a2-c|,…,|an-c|,再将得到的数列继续实施这样的变换,这样的变换可以连续进行多次,并且每次所选择的实数c可以不相同,第k(k∈N*)次变换记为Tk(ck),其中ck为第k次变换时选择的实数.如果通过k次变换后,数列中的各项均为0,则称T1(c1),T2(c2),…,Tk(ck)为“k次归零变换”.查看答案和解析>>
科目:高中数学 来源:2012-2013学年北京市朝阳区高三(上)期中数学试卷(理科)(解析版) 题型:选择题
 ,
, 满足
满足 =1,
=1, =2,且(
=2,且(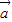 +
+ )⊥
)⊥ ,则
,则 与
与 的夹角为( )
的夹角为( )
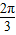
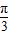

查看答案和解析>>
科目:高中数学 来源:2012-2013学年辽宁省实验中学高三(上)第二次月考数学试卷(理科)(解析版) 题型:解答题
 ,且
,且 •
• =6,
=6, ,求
,求 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:2012-2013学年辽宁省实验中学高三(上)第二次月考数学试卷(理科)(解析版) 题型:选择题
 上是减函数,则b的取值范围是( )
上是减函数,则b的取值范围是( )查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省宿迁中学高三(上)第二次调研数学试卷(解析版) 题型:填空题
 ,其前n项的和是
,其前n项的和是 ,则在平面直角坐标系中,直线(n+1)x+y+n=0在y轴上的截距为 .
,则在平面直角坐标系中,直线(n+1)x+y+n=0在y轴上的截距为 .查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省重点中学高二(上)期中数学试卷(理科)(解析版) 题型:选择题
 (如图②),则图①中的水面高度为( )
(如图②),则图①中的水面高度为( )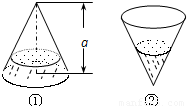
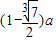

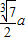
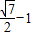 )a
)a查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com