练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数f（x）=x3+ax2+（a+6）x+1有极大值和极小值，则a的取值范围是 ．

    【答案】（﹣∞，﹣3）∪（6，+∞）
    【解析】解：函数f（x）=x3+ax2+（a+6）x+1，所以函数f′（x）=3x2+2ax+（a+6）， 因为函数有极大值和极小值，所以导函数有两个不相等的实数根，即△＞0，
    （2a）2﹣4×3×（a+6）＞0，解得：a∈（﹣∞，﹣3）∪（6，+∞）．
    所以答案是：（﹣∞，﹣3）∪（6，+∞）．
    【考点精析】关于本题考查的二次函数的性质和函数的极值，需要了解当时，抛物线开口向上，函数在上递减，在上递增；当时，抛物线开口向下，函数在上递增，在上递减；极值反映的是函数在某一点附近的大小情况才能得出正确答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】将函数y=sinx的图象上每个点的横坐标变为原来的 倍（纵坐标不变），再将得到的图象向左平移 个单位长度，所得图象的函数解析式为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】f（x），g（x）分别是定义在R上的奇函数和偶函数，当x＜0时，f′（x）g（x）+f（x）g′（x）＜0且f（﹣1）=0则不等式f（x）g（x）＜0的解集为（ ）
    A.（﹣1，0）∪（1，+∞）
    B.（﹣1，0）∪（0，1）
    C.（﹣∞，﹣1）∪（1，+∞）
    D.（﹣∞，﹣1）∪（0，1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数f（x）=2sin（ωx+φ）（ω＞0，﹣ ＜φ＜ ）的部分图象如图所示，将f（x）的图象向左平移 个单位后的解析式为（ ）
    A.y=2sin（2x﹣ ）
    B.y=2sin（2x+ ）
    C.y=2sin（2x）
    D.y=2sin（2x+ ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】靖国神社是日本军国主义的象征.中国人民珍爱和平，所以要坚决反对日本军国主义. 2013年12月26日日本首相安倍晋三悍然参拜靖国神社，此举在世界各国激起舆论的批评.某报的环球舆情调查中心对中国大陆七个代表性城市的1000个普通民众展开民意调查. 某城市调查体统计结果如下表：

    　　

    性别

    中国政府是否

    需要在钓鱼岛和其他争议

    问题上持续对日强硬

    男

    女

    需要

    50

    250

    不需要

    100

    150

    (1) 试估计这七个代表性城市的普通民众中，认为 “中国政府需要在钓鱼岛和其他争议问题上持续对日强硬” 的民众所占比例；

    (2) 能否有以上的把握认为这七个代表性城市的普通民众的民意与性别有关？

    (3) 从被调查认为“中国政府需要在钓鱼岛和其他争议问题上持续对日强硬” 的民众中，采用分层抽样的方式抽取6人做进一步的问卷调查，然后在这6人中用简单随机抽样方法抽取2人进行电视专访，记被抽到的2人中女性的人数为，求的分布列.

    附：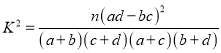

    0.050

    0.010

    0.001

    3.841

    6.635

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四边形ABCD中，AB⊥AD，AD∥BC，AD＝6，BC＝2AB＝4，E，F分别在BC，AD上，EF∥AB.现将四边形ABCD沿EF折起，使平面ABEF⊥平面EFDC.

    （Ⅰ）若BE＝1，是否在折叠后的线段AD上存在一点P，且，使CP∥平面ABEF？若存在，求出λ的值，若不存在，说明理由；

    （Ⅱ）求三棱锥A－CDF的体积的最大值，并求出此时二面角E－AC－F的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】数列{an}满足a1=1，an+1= （n∈N*）．
    （1）计算a2 ， a3 ， a4 ， 并由此猜想通项公式an；
    （2）用数学归纳法证明（1）中的猜想．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x2+2ax+a+1．
    （1）当a=1时，求函数在区间[﹣2，3]上的值域；
    （2）函数f（x）在[﹣5，5]上单调，求实数a的取值范围；
    （3）求函数f（x）在[0，2]上的最小值g（a）的解析式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学校拟建一块周长为400m的操场如图所示，操场的两头是半圆形，中间区域是矩形，学生做操一般安排在矩形区域，为了能让学生的做操区域尽可能大，试问如何设计矩形的长和宽？

    查看答案和解析>>

    同步练习册答案