
分析 根据已知中,$\frac{1}{1×2}=\frac{1}{1}-\frac{1}{2}$,$\frac{1}{2×3}=\frac{1}{2}-\frac{1}{3}$,$\frac{1}{3×4}=\frac{1}{3}-\frac{1}{4}$.分析分母的变化规律,可得$\frac{1}{n(n+1)}$=$\frac{1}{n}-\frac{1}{n+1}$,根据上述结论,利用裂项相消法,可得到两个式子的值;
解答 解:∵$\frac{1}{1×2}=\frac{1}{1}-\frac{1}{2}$,
$\frac{1}{2×3}=\frac{1}{2}-\frac{1}{3}$,
$\frac{1}{3×4}=\frac{1}{3}-\frac{1}{4}$.
…
归纳可得:$\frac{1}{n}-\frac{1}{n+1}$,
(1)$\frac{1}{(x+1)(x+2)}+\frac{1}{(x+2)(x+3)}+\frac{1}{(x+3)(x+4)}$=$\frac{1}{(x+1)}-\frac{1}{(x+2)}+\frac{1}{(x+2)}-\frac{1}{(x+3)}+\frac{1}{(x+3)}-\frac{1}{(x+4)}$=$\frac{1}{(x+1)}-\frac{1}{(x+4)}$=$\frac{3}{{x}^{2}+5x+4}$;
(2)∵$\sqrt{a-1}$+(ab-2)2=0,
∴a-1=0,ab-2=0,
∴a=1,b=2,
∴$\frac{1}{ab}+\frac{1}{(a+1)(b+1)}+\frac{1}{(a+2)(b+2)}$+…+$\frac{1}{(a+2016)(b+2016)}$=$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2017×2018}$=$\frac{1}{1}-\frac{1}{2}$+$\frac{1}{2}-\frac{1}{3}$+$\frac{1}{3}-\frac{1}{4}$+…+$\frac{1}{2017}-\frac{1}{2018}$=$1-\frac{1}{2018}$=$\frac{2017}{2018}$,
故答案为:$\frac{1}{n}-\frac{1}{n+1}$
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | {0,1} | C. | {1,2} | D. | {-2,-1,0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
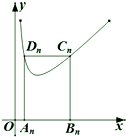 如图,矩形AnBnCnDn的一边AnBn在x轴上,另外两个顶点Cn,Dn在函数f(x)=x+$\frac{1}{x}$(x>0)的图象上.若点Bn的坐为(n,0)(n≥2,n∈N+),记矩形AnBnCnDn的周长为an,则${a_2}•{2^{\frac{a_2}{4}}}+{a_3}•{2^{\frac{a_3}{4}}}+{a_4}•{2^{\frac{a_4}{4}}}…+{a_{10}}•{2^{\frac{{{a_{10}}}}{4}}}$=( )
如图,矩形AnBnCnDn的一边AnBn在x轴上,另外两个顶点Cn,Dn在函数f(x)=x+$\frac{1}{x}$(x>0)的图象上.若点Bn的坐为(n,0)(n≥2,n∈N+),记矩形AnBnCnDn的周长为an,则${a_2}•{2^{\frac{a_2}{4}}}+{a_3}•{2^{\frac{a_3}{4}}}+{a_4}•{2^{\frac{a_4}{4}}}…+{a_{10}}•{2^{\frac{{{a_{10}}}}{4}}}$=( )| A. | 9×213 | B. | 9×214-32 | C. | 9×214-24 | D. | 9×213+24 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com