
已知箱中装有4个白球和5个黑球,且规定:取出一个白球的2分,取出一个黑球的1分.现从该箱中任取(无放回,且每球取到的机会均等)3个球,记随机变量X为取出3球所得分数之和.
(Ⅰ)求X的分布列; (Ⅱ)求X的数学期望E(X).
科目:高中数学 来源: 题型:解答题
袋中有大小、形状相同的红、黑球各一个,现一次有放回地随机摸取3次,每次摸取一个球。
(1)试问:一共有多少种不同的结果?请列出所有可能的结果;
(2)若摸到红球时得2分,摸到黑球时得1分,求3次摸球所得总分为5的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)
某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组 ,第2组
,第2组 ,第3组
,第3组 ,第4组
,第4组 ,第5组
,第5组 得到的频率分布直方图如图所示
得到的频率分布直方图如图所示
(1)分别求第3,4,5组的频率;
(2)若该校决定在第3,4,5 组中用分层抽样的方法抽取6名学生进入第二轮面试,
①已知学生甲和学生乙的成绩均在第3组,求学生甲和学生乙同时进入第二轮面试的概率;
②学校决定在这6名学生中随机抽取2名学生接受考官 的面试,第4组中有
的面试,第4组中有 名学生被考官
名学生被考官 面试,求
面试,求 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)在某学校组织的一次篮球定点投篮训练中,规定每人最多投 次:在
次:在 处每投进一球得
处每投进一球得 分,在
分,在 处每投进一球得
处每投进一球得 分;如果前两次得分之和超过
分;如果前两次得分之和超过 分即停止投篮,否则投第三次.某同学在
分即停止投篮,否则投第三次.某同学在 处的命中率
处的命中率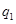 为
为 ,在
,在 处的命中率为
处的命中率为 ,该同学选择先在
,该同学选择先在 处投一球,以后都在
处投一球,以后都在 处投,用
处投,用 表示该同学投篮训练结束后所得的总分,其分布列为
表示该同学投篮训练结束后所得的总分,其分布列为
 | 0 | 2 | 3 | 4 | 5 |
 |  |  |  | 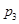 |  |
 的值;
的值; (2) 求随机变量
(2) 求随机变量 的数学期望
的数学期望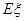 ;
; 处投篮得分超过
处投篮得分超过 分与选择上述方式投篮得分超过
分与选择上述方式投篮得分超过 分的概率的大小.
分的概率的大小. 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
盒中有6只灯泡,其中2只次品,4只正品,有放回地从中任取两次,每次取一只,试求下列事件的概率:(1)取到的2只都是次品;(2)取到的2只中正品、次品各一只;
(3)取到的2只中至少有一只正品.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
.已知关于x的一元二次方程x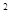 -2(a-2)x-b
-2(a-2)x-b +16=0.
+16=0.
(1)若a、b是一枚骰子先后投掷两次所得到的点数,求方程有两个正实数根的概率;
(2)若a∈[2,6],b∈[0,4],求一元二次方程没有实数根的概率
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在今年伦敦奥运会期间,来自美国和英国的共计6名志愿者被随机地平均分配到跳水、篮球、体操这三个岗位服务,且跳水岗位至少有一名美国志愿者的概率是 .
.
(Ⅰ)求6名志愿者中来自美国、英国的各几人;
(Ⅱ)求篮球岗位恰好美国人、英国人各一人的概率.
(Ⅲ)设随机变量 为在体操岗位服务的美国志愿者的个数,求
为在体操岗位服务的美国志愿者的个数,求 的分布列及期望
的分布列及期望
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示.
(Ⅰ)分别求第3,4,5组的频率;
(Ⅱ)若该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试.
(1)已知学生甲和学生乙的成绩均在第三组,求学生甲和学生乙同时进入第二轮面试的概率;
(2)学校决定在这6名学生中随机抽取2名学生接受考官D的面试,第4组中有 名学生被考官D面试,求
名学生被考官D面试,求 的分布列和数学期望
的分布列和数学期望
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个口袋中装有大小和质地都相同的白球和红球共7个, 其中白球个数不少于红球个数.依次从口袋中任取一球,如果取到红球,那么继续取球,且取出的红球不放回;如果取到白球,就停止取球.记取球的次数为随机变量X.若P(X=2)=
其中白球个数不少于红球个数.依次从口袋中任取一球,如果取到红球,那么继续取球,且取出的红球不放回;如果取到白球,就停止取球.记取球的次数为随机变量X.若P(X=2)= .
.
(1)求口袋中的白球个数;
(2)求 X的概率分布与数学期望.
X的概率分布与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com