
【题目】已知函数f(x)=|x﹣a|﹣|x﹣5|.
(1)当a=2时,求证:﹣3≤f(x)≤3;
(2)若关于x的不等式f(x)≤x2﹣8x+20在R恒成立,求实数a的取值范围.
【答案】(1)证明见解析.(2)![]()
【解析】
(1)![]() 代入,利用绝对值不等式的性质可得
代入,利用绝对值不等式的性质可得![]() ,进而得证;
,进而得证;
(2)分![]() 及
及![]() 两种情况讨论,每种情况下都把函数f(x)化为分段函数的形式,再根据题意转化为关于
两种情况讨论,每种情况下都把函数f(x)化为分段函数的形式,再根据题意转化为关于![]() 的不等式,每种情况解出后最后取并集即可.
的不等式,每种情况解出后最后取并集即可.
(1)证明:当a=2时,f(x)=|x﹣2|﹣|x﹣5|,
∴||x﹣2|﹣|x﹣5||![]() |x﹣2﹣(x﹣5)|=3,
|x﹣2﹣(x﹣5)|=3,
∴﹣3![]() |x﹣2|﹣|x﹣5|
|x﹣2|﹣|x﹣5|![]() 3,即﹣3
3,即﹣3![]() f(x)
f(x)![]() 3;
3;
(2)解:f(x)=|x﹣a|﹣|x﹣5|,
①当a![]() 5时,
5时,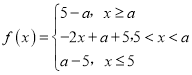 ,则f(x)max=a﹣5,且y=x2﹣8x+20=x2﹣8x+16+4=(x﹣4)2+4
,则f(x)max=a﹣5,且y=x2﹣8x+20=x2﹣8x+16+4=(x﹣4)2+4![]() 4,
4,
要使f(x)![]() x2﹣8x+20在R恒成立,则只需4
x2﹣8x+20在R恒成立,则只需4![]() a﹣5,则a
a﹣5,则a![]() 9,此时5
9,此时5![]() a
a![]() 9;
9;
②当a<5时,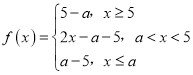 ,
,
需要 恒成立,
恒成立,
∴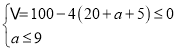 ,
,
∴![]() ,
,
综合①②可知,0![]() a
a![]() 9,即实数a的取值范围为[0,9].
9,即实数a的取值范围为[0,9].


科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC﹣A1B1C1中,AB⊥BC,BB1![]() BC,D是CC1的中点.
BC,D是CC1的中点.

(1)证明:B1C⊥平面ABD;
(2)若AB=BC,E是A1C1的中点,求二面角A﹣BD﹣E的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两厂均生产某种零件.根据长期检测结果:甲、乙两厂生产的零件质量(单位:![]() )均服从正态分布
)均服从正态分布![]() ,在出厂检测处,直接将质量在
,在出厂检测处,直接将质量在![]() 之外的零件作为废品处理,不予出厂;其它的准予出厂,并称为正品.
之外的零件作为废品处理,不予出厂;其它的准予出厂,并称为正品.
(1)出厂前,从甲厂生产的该种零件中抽取10件进行检查,求至少有1片是废品的概率;
(2)若规定该零件的“质量误差”计算方式为:该零件的质量为![]() ,则“质量误差”
,则“质量误差”![]() .按标准,其中“优等”、“一级”、“合格”零件的“质量误差”范围分别是
.按标准,其中“优等”、“一级”、“合格”零件的“质量误差”范围分别是![]() ,
,![]() 、
、![]() (正品零件中没有“质量误差”大于
(正品零件中没有“质量误差”大于![]() 的零件),每件价格分别为75元、65元、50元.现分别从甲、乙两厂生产的正品零件中随机抽取100件,相应的“质量误差”组成的样本数据如下表(用这个样本的频率分布估计总体分布,将频率视为概率):
的零件),每件价格分别为75元、65元、50元.现分别从甲、乙两厂生产的正品零件中随机抽取100件,相应的“质量误差”组成的样本数据如下表(用这个样本的频率分布估计总体分布,将频率视为概率):
质量误差 |
|
|
|
|
|
|
|
甲厂频数 | 10 | 30 | 30 | 5 | 10 | 5 | 10 |
乙厂频数 | 25 | 30 | 25 | 5 | 10 | 5 | 0 |
(ⅰ)记甲厂该种规格的2件正品零件售出的金额为![]() (元),求
(元),求![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
(ⅱ)由上表可知,乙厂生产的该规格的正品零件只有“优等”、“一级”两种,求5件该规格零件售出的金额不少于360元的概率.
附:若随机变量![]() .则
.则![]() ;
;![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场进行抽奖促销活动,抽奖箱中有大小完全相同的4个小球,分别标有“A”“B”“C”“D”.顾客从中任意取出1个球,记下上面的字后放回箱中,再从中任取1个球,重复以上操作,最多取4次,并规定若取出“D”字球,则停止取球.获奖规则如下:依次取到标有““A”“B”“C”“D”字的球为一等奖;不分顺序取到标有“A”“B”“C”“D”字的球,为二等奖;取到的4个球中有标有“A”“B”“C”三个字的球为三等奖.
(1)求分别获得一、二、三等奖的概率;
(2)设摸球次数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年底,湖北省武汉市等多个地区陆续出现感染新型冠状病毒肺炎的患者.为及时有效地对疫情数据进行流行病学统计分析,某地研究机构针对该地实际情况,根据该地患者是否有武汉旅行史与是否有确诊病例接触史,将新冠肺炎患者分为四类:有武汉旅行史(无接触史),无武汉旅行史(无接触史),有武汉旅行史(有接触史)和无武汉旅行史(有接触史),统计得到以下相关数据.
(1)请将列联表填写完整:
有接触史 | 无接触史 | 总计 | |
有武汉旅行史 | 27 | ||
无武汉旅行史 | 18 | ||
总计 | 27 | 54 |
(2)能否在犯错误的概率不超过0.025的前提下认为有武汉旅行史与有确诊病例接触史有关系?
附:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,过椭圆C:![]() 上一点P作x轴的垂线,垂足为
上一点P作x轴的垂线,垂足为![]() ,已知
,已知![]() ,
,![]() 分别为椭圆C的左、右焦点,A,B分别是椭圆C的右顶点、上顶点,且
分别为椭圆C的左、右焦点,A,B分别是椭圆C的右顶点、上顶点,且![]() ,
,![]() .
.
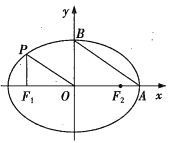
(1)求椭圆C的方程;
(2)过点![]() 的直线l交椭圆C于M,N两点,记直线PM,PN,MN的斜率分别为
的直线l交椭圆C于M,N两点,记直线PM,PN,MN的斜率分别为![]() ,问:
,问:![]() 是否为定值?请说明理由.
是否为定值?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天上有些恒星的亮度是会变化的,其中一种称为造父(型)变星,本身体积会膨胀收缩造成亮度周期性的变化.第一颗被描述的经典造父变星是在1784年.
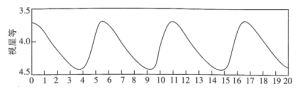
上图为一造父变星的亮度随时间的周期变化图,其中视星等的数值越小,亮度越高,则此变星亮度变化的周期、最亮时视星等,分别约是( )
A.5.5,3.7B.5.4,4.4C.6.5,3.7D.5.5,4.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com