Question

有两个相同的直三棱柱,高为,底面三角形的三边长分别为3a、4a、5a(a＞0),用它们拼成一个三棱柱或四棱柱,在所有可能的情形中,全面积最小的是一个四棱柱,则a的取值范围是___________________.

Answer 1

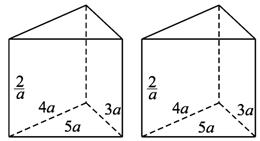
解析：本题考查棱柱的概念及性质,考查空间想象能力、分类讨论的思想和割补思想.

由题意,拼成的三棱柱或四棱柱的所有可能情况共7种:

(1)底面是边长为3a、4a的矩形,侧棱长为的直四棱柱.全面积S₁=24a²+28.(2)底面是边长为5a、4a的平行四边形,侧棱长为的直四棱柱.全面积为24a²+36.(3)底面是边长为5a、3a的平行四边形,侧棱长为的直四棱柱.全面积为24a²+32.(4)底面是边长为3a、4a的四边形,侧棱长为的直四棱柱.全面积为24a²+28.(5)底面是边长分别为5a、5a、6a的三角形,侧棱长为的直三棱柱,全面积为24a²+32.(6)底面是边长分别为5a、5a、8a的三角形,侧棱长为的直三棱柱,全面积为24a²+36.(7)底面是边长分别为3a、4a、5a的三角形,侧棱长为的直三棱柱,全面积为12a²+48.因为全面积最小的是一个四棱柱,故24a²+28＜12a²+48且a＞0,解得0＜a＜.

答案：0＜a＜