
分析 由条件利用函数y=Asin(ωx+φ)的图象变换规律,求得φ的最小值.
解答 解:函数y=sin2x的图象向左平移φ(φ>0)个单位,若所得的图象对应的函数解析式为y=sin2(x+φ),
再根据所得函数的图象过点($\frac{π}{6}$,$\frac{\sqrt{3}}{2}$),可得sin2($\frac{π}{6}$+φ)=$\frac{\sqrt{3}}{2}$,则φ的最小值满足2φ+$\frac{π}{3}$=$\frac{2π}{3}$,
求得φ的最小值为$\frac{π}{6}$,
故答案为:$\frac{π}{6}$.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,根据三角函数的值求角,属于基础题.


 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:解答题
 某个公司调查统计它的员工每周参与体育锻炼的时间,样本容量为100人,将调查结果统计为频率分布直方图,如图.我们将每周体育锻炼时间不低于150分钟的人称为“勤于锻炼者”,并将有关性别的信息统计到表中.
某个公司调查统计它的员工每周参与体育锻炼的时间,样本容量为100人,将调查结果统计为频率分布直方图,如图.我们将每周体育锻炼时间不低于150分钟的人称为“勤于锻炼者”,并将有关性别的信息统计到表中.| “勤于锻炼者” | 非“勤于锻炼者” | 合计 | |
| 男 | 25 | 70 | |
| 女 | |||
| 合计 |
| p(X2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
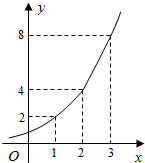 如图所示的是某海域浒苔蔓延的面积(m2)与时间x(天)的满足函数关系y=ax,有以下叙述:
如图所示的是某海域浒苔蔓延的面积(m2)与时间x(天)的满足函数关系y=ax,有以下叙述:| A. | ①② | B. | ①②④ | C. | ①②③ | D. | ②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com