
ЁОЬтФПЁПЫОЛњдкПЊЛњЖЏГЕЪБЪЙгУЪжЛњЪЧЮЅЗЈааЮЊЃЌЛсДцдкбЯжиЕФАВШЋвўЛМЃЌЮЃМАздМККЭЫћШЫЕФЩњУќ. ЮЊСЫбаОПЫОЛњПЊГЕЪБЪЙгУЪжЛњЕФЧщПіЃЌНЛОЏВПУХЕїВщСЫ![]() УћЛњЖЏГЕЫОЛњЃЌЕУЕНвдЯТЭГМЦЃКдк
УћЛњЖЏГЕЫОЛњЃЌЕУЕНвдЯТЭГМЦЃКдк![]() УћФаадЫОЛњжаЃЌПЊГЕЪБЪЙгУЪжЛњЕФга
УћФаадЫОЛњжаЃЌПЊГЕЪБЪЙгУЪжЛњЕФга![]() ШЫЃЌПЊГЕЪБВЛЪЙгУЪжЛњЕФга
ШЫЃЌПЊГЕЪБВЛЪЙгУЪжЛњЕФга![]() ШЫЃЛдк
ШЫЃЛдк![]() УћХЎадЫОЛњжаЃЌПЊГЕЪБЪЙгУЪжЛњЕФга
УћХЎадЫОЛњжаЃЌПЊГЕЪБЪЙгУЪжЛњЕФга![]() ШЫЃЌПЊГЕЪБВЛЪЙгУЪжЛњЕФга
ШЫЃЌПЊГЕЪБВЛЪЙгУЪжЛњЕФга![]() ШЫЃЎ
ШЫЃЎ
ЃЈ1ЃЉЭъГЩЯТУцЕФ![]() СаСЊБэЃЌВЂХаЖЯЪЧЗёга
СаСЊБэЃЌВЂХаЖЯЪЧЗёга![]() ЕФАбЮеШЯЮЊПЊГЕЪБЪЙгУЪжЛњгыЫОЛњЕФадБ№гаЙиЃЛ
ЕФАбЮеШЯЮЊПЊГЕЪБЪЙгУЪжЛњгыЫОЛњЕФадБ№гаЙиЃЛ
ПЊГЕЪБЪЙгУЪжЛњ | ПЊГЕЪБВЛЪЙгУЪжЛњ | КЯМЦ | |
ФаадЫОЛњШЫЪ§ | |||
ХЎадЫОЛњШЫЪ§ | |||
КЯМЦ |
ЃЈ2ЃЉвдЩЯЪіЕФбљБОЪ§ОнРДЙРМЦзмЬхЃЌЯжНЛОЏВПУХДгЕРТЗЩЯааЪЛЕФДѓСПЛњЖЏГЕжаЫцЛњГщМь3СОЃЌМЧет3СОГЕжаЫОЛњЮЊФаадЧвПЊГЕЪБЪЙгУЪжЛњЕФГЕСОЪ§ЮЊ![]() ЃЌШєУПДЮГщМьЕФНсЙћЖМЯрЛЅЖРСЂЃЌЧѓ
ЃЌШєУПДЮГщМьЕФНсЙћЖМЯрЛЅЖРСЂЃЌЧѓ![]() ЕФЗжВМСаКЭЪ§бЇЦкЭћ
ЕФЗжВМСаКЭЪ§бЇЦкЭћ![]() ЃЎ
ЃЎ
ВЮПМЙЋЪНгыЪ§ОнЃК
ВЮПМЪ§ОнЃК
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ВЮПМЙЋЪН
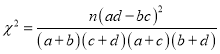 span>ЃЌЦфжа
span>ЃЌЦфжа![]() .
.
ЁОД№АИЁПЃЈ1ЃЉСаСЊБэМћНтЮіЃЌгаЃЛЃЈ2ЃЉЗжВМСаМћНтЮіЃЌ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнвбжЊЪ§ОнМДПЩЕУЕНСаСЊБэЃЛМЦЫуГі![]() ЃЌЖдБШСйНчжЕБэПЩЕУЕННсЙћЃЛЃЈ2ЃЉгЩбљБОЙРМЦзмЬхЫМЯыЃЌПЩЕУЕНЫцЛњГщМь
ЃЌЖдБШСйНчжЕБэПЩЕУЕННсЙћЃЛЃЈ2ЃЉгЩбљБОЙРМЦзмЬхЫМЯыЃЌПЩЕУЕНЫцЛњГщМь![]() СОЃЌЫОЛњЮЊФаадЧвПЊГЕЪЙгУЪжЛњЕФИХТЪЮЊ
СОЃЌЫОЛњЮЊФаадЧвПЊГЕЪЙгУЪжЛњЕФИХТЪЮЊ![]() ЃЌПЩжЊ
ЃЌПЩжЊ![]() ЃЌгЩЖўЯюЗжВМИХТЪЙЋЪНПЩМЦЫуЕУЕНУПИіШЁжЕЫљЖдгІЕФИХТЪЃЌДгЖјЕУЕНЗжВМСаЃЛгЩЖўЯюЗжВМЪ§бЇЦкЭћМЦЫуЙЋЪНПЩЕУ
ЃЌгЩЖўЯюЗжВМИХТЪЙЋЪНПЩМЦЫуЕУЕНУПИіШЁжЕЫљЖдгІЕФИХТЪЃЌДгЖјЕУЕНЗжВМСаЃЛгЩЖўЯюЗжВМЪ§бЇЦкЭћМЦЫуЙЋЪНПЩЕУ![]() .
.
ЃЈ1ЃЉгЩвбжЊЪ§ОнПЩЕУ![]() СаСЊБэШчЯТЃК
СаСЊБэШчЯТЃК
ПЊГЕЪБЪЙгУЪжЛњ | ПЊГЕЪБВЛЪЙгУЪжЛњ | КЯМЦ | |
ФаадЫОЛњШЫЪ§ |
|
|
|
ХЎадЫОЛњШЫЪ§ |
|
|
|
КЯМЦ |
|
|
|
![]()
![]() га
га![]() ЕФАбЮеШЯЮЊПЊГЕЪБЪЙгУЪжЛњгыЫОЛњЕФадБ№гаЙи
ЕФАбЮеШЯЮЊПЊГЕЪБЪЙгУЪжЛњгыЫОЛњЕФадБ№гаЙи
ЃЈ2ЃЉЫцЛњГщМь![]() СОЃЌЫОЛњЮЊФаадЧвПЊГЕЪБЪЙгУЪжЛњЕФИХТЪ
СОЃЌЫОЛњЮЊФаадЧвПЊГЕЪБЪЙгУЪжЛњЕФИХТЪ![]()
гаЬтвтПЩжЊЃК![]() ПЩШЁжЕЪЧ
ПЩШЁжЕЪЧ![]() ЃЌЧв
ЃЌЧв![]()
 ЃЛ
ЃЛ ЃЛ
ЃЛ
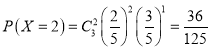 ЃЛ
ЃЛ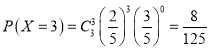
дђ![]() ЕФЗжВМСаЮЊЃК
ЕФЗжВМСаЮЊЃК
|
|
|
|
|
|
|
|
|
|
Ъ§бЇЦкЭћ![]()


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНааЫФБпаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЙ§
ЃЌЙ§![]() Еузї
Еузї![]() ЕФДЙЯпЃЌНЛ
ЕФДЙЯпЃЌНЛ![]() ЕФбгГЄЯпгкЕу
ЕФбгГЄЯпгкЕу![]() ЃЌ
ЃЌ![]() .СЌНс
.СЌНс![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() ЃЌШчЭМ1ЃЌНЋ
ЃЌШчЭМ1ЃЌНЋ![]() би
би![]() елЦ№ЃЌЪЙЕУЕу
елЦ№ЃЌЪЙЕУЕу![]() ЕНДяЕу
ЕНДяЕу![]() ЕФЮЛжУЃЌШчЭМ2.
ЕФЮЛжУЃЌШчЭМ2.
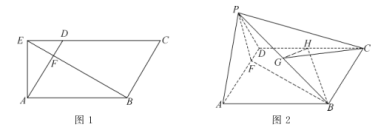
ЃЈ1ЃЉжЄУїЃКЦНУц![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШє![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌЧвЦНУц
ЕФжаЕуЃЌЧвЦНУц![]() ЦНУц
ЦНУц![]() ЃЌЧѓШ§РтзЖ
ЃЌЧѓШ§РтзЖ![]() ЕФЬхЛ§.
ЕФЬхЛ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЪЧгЩжБЯп
ЪЧгЩжБЯп![]() в§ГіЕФШ§ИіВЛжиКЯЕФАыЦНУцЃЌЦфжаЖўУцНЧ
в§ГіЕФШ§ИіВЛжиКЯЕФАыЦНУцЃЌЦфжаЖўУцНЧ![]() ДѓаЁЮЊ60ЁуЃЌ
ДѓаЁЮЊ60ЁуЃЌ![]() дкЖўУцНЧ
дкЖўУцНЧ![]() ФкШЦжБЯп
ФкШЦжБЯп![]() а§зЊЃЌдВ
а§зЊЃЌдВ![]() дк
дк![]() ФкЃЌЧвдВ
ФкЃЌЧвдВ![]() дк
дк![]() ЃЌ
ЃЌ![]() ФкЕФЩфгАЗжБ№ЮЊЭждВ
ФкЕФЩфгАЗжБ№ЮЊЭждВ![]() ЃЌ
ЃЌ![]() .МЧЭждВ
.МЧЭждВ![]() ЃЌ
ЃЌ![]() ЕФРыаФТЪЗжБ№ЮЊ
ЕФРыаФТЪЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
ЕФШЁжЕЗЖЮЇЪЧЃЈ ЃЉ
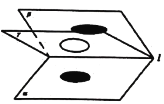
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшКЏЪ§![]() .
.
(1)ШєЧњЯп![]() гы
гы![]() дкЫќУЧЕФНЛЕу
дкЫќУЧЕФНЛЕу![]() ДІгаЯрЭЌЕФЧаЯп,ЧѓЪЕЪ§a,bЕФжЕ;
ДІгаЯрЭЌЕФЧаЯп,ЧѓЪЕЪ§a,bЕФжЕ;
(2)ЕБ![]() ЪБ,ШєКЏЪ§
ЪБ,ШєКЏЪ§![]() дкЧјМф
дкЧјМф![]() ФкЧЁгаСНИіСуЕу,ЧѓЪЕЪ§ЕФШЁжЕЗЖЮЇ.
ФкЧЁгаСНИіСуЕу,ЧѓЪЕЪ§ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭждВ![]() ЕФжааФдкзјБъдЕуЃЌНЙЕу
ЕФжааФдкзјБъдЕуЃЌНЙЕу![]() дк
дк![]() жсЩЯЃЌЙ§зјБъдЕуЕФжБЯп
жсЩЯЃЌЙ§зјБъдЕуЕФжБЯп![]() НЛ
НЛ![]() гк
гк![]() СНЕуЃЌ
СНЕуЃЌ![]() ЃЌ
ЃЌ![]() УцЛ§ЕФзюДѓжЕЮЊ
УцЛ§ЕФзюДѓжЕЮЊ![]()
ЃЈ1ЃЉЧѓЭждВ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉ![]() ЪЧЭждВЩЯгы
ЪЧЭждВЩЯгы![]() ВЛжиКЯЕФвЛЕуЃЌжЄУїЃКжБЯп
ВЛжиКЯЕФвЛЕуЃЌжЄУїЃКжБЯп![]() ЕФаБТЪжЎЛ§ЮЊЖЈжЕЃЛ
ЕФаБТЪжЎЛ§ЮЊЖЈжЕЃЛ
ЃЈ3ЃЉЕБЕу![]() дкЕквЛЯѓЯоЪБЃЌ
дкЕквЛЯѓЯоЪБЃЌ![]() жсЃЌДЙзуЮЊ
жсЃЌДЙзуЮЊ![]() ЃЌСЌНг
ЃЌСЌНг![]() ВЂбгГЄНЛ
ВЂбгГЄНЛ![]() гкЕу
гкЕу![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФУцЛ§ЕФзюДѓжЕ.
ЕФУцЛ§ЕФзюДѓжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙ§ХзЮяЯпx2ЃН2py(p>0)ЕФНЙЕуЃЌаБТЪЮЊ![]() ЕФжБЯпНЛХзЮяЯпгкA(x1ЃЌy1)ЃЌB(x2ЃЌy2)(x1<x2)СНЕуЃЌЧв|AB|ЃН9.
ЕФжБЯпНЛХзЮяЯпгкA(x1ЃЌy1)ЃЌB(x2ЃЌy2)(x1<x2)СНЕуЃЌЧв|AB|ЃН9.
(1)ЧѓИУХзЮяЯпЕФЗНГЬЃЛ
(2)OЮЊзјБъдЕуЃЌCЮЊХзЮяЯпЩЯвЛЕуЃЌШє![]() ,ЧѓІЫЕФжЕ.
,ЧѓІЫЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊдВCЙ§СНЕуAЃЈ0ЃЌ4ЃЉЃЌBЃЈ4ЃЌ6ЃЉЃЌЧвдВаФдкжБЯпxЉ2yЉ2=0ЩЯЃЎ
ЃЈ1ЃЉЧѓдВCЕФЗНГЬЃЛ
ЃЈ2ЃЉШєжБЯпlЙ§дЕуЧвБЛдВCНиЕУЕФЯвГЄЮЊ6ЃЌЧѓжБЯпlЕФЗНГЬЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮ![]() ЮЊе§ЗНаЮЃЌ
ЮЊе§ЗНаЮЃЌ![]() ЗжБ№ЮЊ
ЗжБ№ЮЊ![]() ЕФжаЕуЃЌвд
ЕФжаЕуЃЌвд![]() ЮЊелКлАб
ЮЊелКлАб![]() елЦ№ЃЌЪЙЕу
елЦ№ЃЌЪЙЕу![]() ЕНДяЕу
ЕНДяЕу![]() ЕФЮЛжУЃЌЧв
ЕФЮЛжУЃЌЧв![]() .
.
ЃЈ1ЃЉжЄУїЃКЦНУц![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓ![]() гыЦНУц
гыЦНУц![]() ЫљГЩНЧЕФе§ЯвжЕ.
ЫљГЩНЧЕФе§ЯвжЕ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]() ЃК
ЃК![]() ЕФзѓгвНЙЕуЗжБ№ЮЊ
ЕФзѓгвНЙЕуЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЃЌзѓгвЖЅЕуЗжБ№ЪЧ
ЃЌзѓгвЖЅЕуЗжБ№ЪЧ![]() ЁЂ
ЁЂ![]() ЃЌГЄжсГЄЮЊ
ЃЌГЄжсГЄЮЊ![]() ЃЌ
ЃЌ![]() ЪЧвддЕуЮЊдВаФЃЌ
ЪЧвддЕуЮЊдВаФЃЌ![]() ЮЊАыОЖЕФдВЕФШЮвЛЬѕжБОЖЃЌЫФБпаЮ
ЮЊАыОЖЕФдВЕФШЮвЛЬѕжБОЖЃЌЫФБпаЮ![]() ЕФУцЛ§зюДѓжЕЮЊ
ЕФУцЛ§зюДѓжЕЮЊ![]() .
.
ЃЈ1ЃЉЧѓЭждВ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉВЛОЙ§дЕуЕФжБЯп![]() ЃК
ЃК![]() гыЭждВНЛгк
гыЭждВНЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЌ
СНЕуЃЌ
ЂйШєжБЯп![]() гы
гы![]() ЕФаБТЪЗжБ№ЮЊ
ЕФаБТЪЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌЧв
ЃЌЧв![]() ЃЌЧѓжЄЃКжБЯп
ЃЌЧѓжЄЃКжБЯп![]() Й§ЖЈЕуЃЌВЂЧѓГіИУЖЈЕуЕФзјБъЃЛ
Й§ЖЈЕуЃЌВЂЧѓГіИУЖЈЕуЕФзјБъЃЛ
ЂкШєжБЯп![]() ЕФаБТЪЪЧжБЯп
ЕФаБТЪЪЧжБЯп![]() ЁЂ
ЁЂ![]() аБТЪЕФЕШБШжаЯюЃЌЧѓ
аБТЪЕФЕШБШжаЯюЃЌЧѓ![]() УцЛ§ЕФШЁжЕЗЖЮЇ.
УцЛ§ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com