
【题目】某公司要了解某商品的年广告费![]() (单位:万元)对年销售额
(单位:万元)对年销售额![]() (单位:万元)的影响,对近4年的年广告费
(单位:万元)的影响,对近4年的年广告费![]() 和年销售额
和年销售额![]() 数据作了初步调研,得到下面的表格:
数据作了初步调研,得到下面的表格:
年广告费 | 2 | 3 | 4 | 5 |
年销售额 | 26 | 39 | 49 | 54 |
用广告费作解释变量,年销售额作预报变量,且![]() 适宜作为年销售额
适宜作为年销售额![]() 关于年广告费
关于年广告费![]() 的回归方程类型.
的回归方程类型.
(1)根据表中数据,建立![]() 关于
关于![]() 的回归方程.
的回归方程.
(2)已知商品的年利润![]() 与
与![]() ,
,![]() 的关系式为
的关系式为![]() ,根据(1)中的结果,估计年广告费
,根据(1)中的结果,估计年广告费![]() 为何值时(小数点后保留两位),年利润的预报值最大?
为何值时(小数点后保留两位),年利润的预报值最大?
(对于数据![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为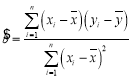 ,
,![]() ).
).
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
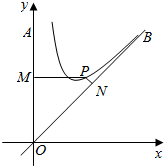
【题目】![]() 直线交x轴于点A,交y轴于点B,抛物线
直线交x轴于点A,交y轴于点B,抛物线![]() (
(![]() )经过点A,交x轴于另一点C,如图所示.
)经过点A,交x轴于另一点C,如图所示.

(1)求抛物线的解析式.
(2)设抛物线的顶点为D,连接BD,AD,CD,动点P在BD上以每秒2个单位长度的速度由点B向点D运动,同时动点Q在线段CA上以每秒3个单位长度的速度由点C向点A运动,当其中一个点到达终点停止运动时,另一个点也随之停止运动,设运动时间为t秒.PQ交线段AD于点E.
①当![]() 时,求t的值;
时,求t的值;
②过点E作![]() ,垂足为点M,过点P作
,垂足为点M,过点P作![]() 交线段AB或AD于点N,当
交线段AB或AD于点N,当![]() 时,求t的值.
时,求t的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明每天上学都需要经过一个有交通信号灯的十字路口.已知十字路口的交通信号灯绿灯亮的时间为40秒,黄灯5秒,红灯45秒.如果小明每天到路口的时间是随机的,则小明上学时到十字路口需要等待的时间不少于20秒的概率是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是南北方向的一条公路,
是南北方向的一条公路,![]() 是北偏东
是北偏东![]() 方向的一条公路,某风景区的一段边界为曲线
方向的一条公路,某风景区的一段边界为曲线![]() .为方便游客光,拟过曲线
.为方便游客光,拟过曲线![]() 上的某点分别修建与公路
上的某点分别修建与公路![]() ,
,![]() 垂直的两条道路
垂直的两条道路![]() ,
,![]() ,且
,且![]() ,
,![]() 的造价分别为5万元
的造价分别为5万元![]() 百米,40万元
百米,40万元![]() 百米,建立如图所示的直角坐标系
百米,建立如图所示的直角坐标系![]() ,则曲线符合函数
,则曲线符合函数![]() 模型,设
模型,设![]() ,修建两条道路
,修建两条道路![]() ,
,![]() 的总造价为
的总造价为![]() 万元,题中所涉及的长度单位均为百米.
万元,题中所涉及的长度单位均为百米.
(1)求![]() 解析式;
解析式;
(2)当![]() 为多少时,总造价
为多少时,总造价![]() 最低?并求出最低造价.
最低?并求出最低造价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,圆
,圆![]() ,以动点
,以动点![]() 为圆心的圆经过点
为圆心的圆经过点![]() ,且圆
,且圆![]() 与圆
与圆![]() 内切.
内切.
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)若直线![]() 过点
过点![]() ,且与曲线
,且与曲线![]() 交于
交于![]() 两点,则在
两点,则在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 轴平分
轴平分![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个大型喷水池的中央有一个强力喷水柱,为了测量喷水柱喷出的水柱的高度,某人在喷水柱正西方向的点A测得水柱顶端的仰角为45°,沿点A向北偏东30°前进100 m到达点B,在B点测得水柱顶端的仰角为30°,则水柱的高度是( )
A. 50 mB. 100 m
C. 120 mD. 150 m
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1为某省2018年1~4月快递业务量统计图,图2是该省2018年1~4月快递业务收入统计图,下列对统计图理解错误的是( )


A. 2018年1~4月的业务量,3月最高,2月最低,差值接近2000万件
B. 2018年1~4月的业务量同比增长率均超过50%,在3月底最高
C. 从两图来看,2018年1~4月中的同一个月的快递业务量与收入的同比增长率并不完全一致
D. 从1~4月来看,该省在2018年快递业务收入同比增长率逐月增长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com