
【题目】如果 ![]() ,
, ![]() 是平面
是平面 ![]() 内所有向量的一组基底,那么( )
内所有向量的一组基底,那么( )
A.若实数 ![]() ,
, ![]() ,使
,使 ![]() ,则
,则 ![]()
B.空间任一向量 ![]() 可以表示为
可以表示为 ![]() ,这里
,这里 ![]() ,
, ![]() 是实数
是实数
C.![]() ,
, ![]() 不一定在平面
不一定在平面 ![]() 内
内
D.对平面 ![]() 内任一向量
内任一向量 ![]() ,使
,使 ![]() 的实数
的实数 ![]() ,
, ![]() 有无数对
有无数对
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足:a3=7,a5+a7=26.{an}的前n项和为Sn . (Ⅰ)求an及Sn;
(Ⅱ)令bn= ![]() (n∈N*),求数列{bn}的前n项和Tn .
(n∈N*),求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,P是四边形ABCD所在平面外的一点,四边形ABCD是∠DAB=60°且边长为a的菱形.侧面PAD为正三角形,其所在平面垂直于底面ABCD.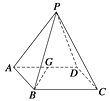
(1)若G为AD边的中点,求证:BG⊥平面PAD;
(2)求证:AD⊥PB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}及等差数列{bn},若a1=3, ![]() (n≥2),a1=b2 , 2a3+a2=b4 ,
(n≥2),a1=b2 , 2a3+a2=b4 ,
(1)证明数列{an﹣2}为等比数列;
(2)求数列{an}及数列{bn}的通项公式;
(3)设数列{anbn}的前n项和为Tn , 求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】咖啡馆配制两种饮料,甲种饮料每杯分别用奶粉、咖啡、糖9g、4g、3g;乙种饮料每杯分别用奶粉、咖啡、糖4g、5g、10g,已知每天使用原料限额为奶粉3600g,咖啡2000g,糖3000g,如果甲种饮料每杯能获利0.7元,乙种饮料每杯能获利1.2元,每天在原料使用的限额内,饮料能全部售完,问咖啡馆每天怎样安排配制饮料获利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{bn}满足bn=| ![]() |,其中a1=2,an+1=
|,其中a1=2,an+1= ![]()
(1)求b1 , b2 , b3 , 并猜想bn的表达式(不必写出证明过程);
(2)设cn= ![]() ,数列|cn|的前项和为Sn , 求证Sn<
,数列|cn|的前项和为Sn , 求证Sn< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】①设三个正实数a , b , c , 满足![]() ,求证:a , b , c一定是某一个三角形的三条边的长;
,求证:a , b , c一定是某一个三角形的三条边的长;
②设n个正实数 a1,a2,...an 满足不等式 ![]() (其中
(其中 ![]() ),求证: a1,a2,...an 中任何三个数都是某一个三角形的三条边的长.
),求证: a1,a2,...an 中任何三个数都是某一个三角形的三条边的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com