
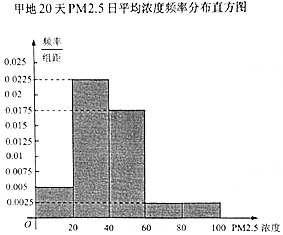
| PM2.5日平均浓度(微克/立方米) | [0,20] | (20,40] | (40,60] | (60,80] | (80,100] |
| 频数(天) | 2 | 3 | 4 | 6 | 5 |
| 满意度等级 | 非常满意 | 满意 | 不满意 |
| PM2.5日平均浓度(微克/立方米) | 不超过20 | 大于20不超过60 | 超过60 |
分析 (1)根据频率分布直方图的画法画图即可,由图比较即可,
(2)设可设乙地这20天中PM2.5日平均浓度不超过40的5天分别为a,b,c,d,e,其中a,b表示居民对空气质量满意度为“非常满意”的两天,列举出从5天任取2天的所有情况和满足至少有一天居民对空气质量满意度为“非常满意“的情况数,代入古典概型概率计算公式,可得答案
解答 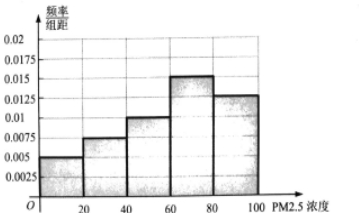 解:(1)如图所示:由图可知:甲地PM2.5日平均浓度的平均值低于乙地PM2.5日平均浓度的平均值,而且甲地的数据比较集中,乙地的数据比较分散,
解:(1)如图所示:由图可知:甲地PM2.5日平均浓度的平均值低于乙地PM2.5日平均浓度的平均值,而且甲地的数据比较集中,乙地的数据比较分散,
(2)由题意,可设乙地这20天中PM2.5日平均浓度不超过40的5天分别为a,b,c,d,e,其中a,b表示居民对空气质量满意度为“非常满意”的两天,则从5天中任取两天共有以下10种情况:(a,b),(a,c),(a,d),(a,e),(b,c),(b,d),(b,e),(c,d),
(c,e),(d,e),其中至少有一天为“非常满意”有以下7种,(a,b),(a,c),
(a,d),(a,e),(b,c),(b,d),(b,e),
所以所求概率P=$\frac{7}{10}$
点评 本题考查概率的求法和频率分布直方图的画法,解题时要认真审题,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
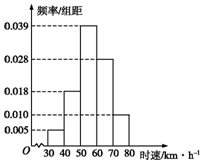 某时段内共有100辆汽车经过某一雷达地区,汽车时速的频率分布直方图如图所示,则时速不低于60km/h的汽车数量为( )
某时段内共有100辆汽车经过某一雷达地区,汽车时速的频率分布直方图如图所示,则时速不低于60km/h的汽车数量为( )| A. | 38 | B. | 28 | C. | 10 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,网格纸上的小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积是( )
如图,网格纸上的小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积是( )| A. | 4+6π | B. | 4+12π | C. | 8+6π | D. | 8+12π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com