
【题目】已知椭圆![]() 的一个顶点为
的一个顶点为![]() ,离心率
,离心率![]() ,直线
,直线![]() 交椭圆于
交椭圆于![]() 、
、![]() 两点.
两点.
(1)若直线![]() 的方程为
的方程为![]() ,求弦
,求弦![]() 的长;
的长;
(2)如果![]() 的重心恰好为椭圆的右焦点
的重心恰好为椭圆的右焦点![]() ,求直线
,求直线![]() 方程的一般式.
方程的一般式.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】中国古代十进制的算筹计数法,在世界数学史上是一个伟大的创造. 算筹实际上是一根根同样长短的小木棍,用算筹表示数1~9的方法如图:例如:163可表示为“![]() ”,27可表示为“
”,27可表示为“![]() ”.现有6根算筹,用来表示不能被10整除的两位数,算筹必须用完,则这样的两位数的个数为_________.
”.现有6根算筹,用来表示不能被10整除的两位数,算筹必须用完,则这样的两位数的个数为_________.

查看答案和解析>>
科目:高中数学 来源: 题型:
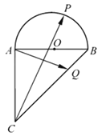
【题目】如图,在等腰直角三角形ABC中,∠CAB=90°,AB=2,以AB为直径在△ABC外作半圆O,P为半圆弧AB上的动点,点Q在斜边BC上,若![]() =
=![]() ,则
,则![]() 的最小值为_______.
的最小值为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 是各项都不为0的无穷数列,对任意的n≥3,n
是各项都不为0的无穷数列,对任意的n≥3,n![]() ,
,![]()
![]() 恒成立.
恒成立.
(1)如果![]() ,
,![]() ,
,![]() 成等差数列,求实数
成等差数列,求实数![]() 的值;
的值;
(2)已知![]() =1.①求证:数列
=1.①求证:数列![]() 是等差数列;②已知数列
是等差数列;②已知数列![]() 中,
中,![]() .数列
.数列![]() 是公比为q的等比数列,满足
是公比为q的等比数列,满足![]() ,
,![]() ,
,![]() (i
(i![]() ).求证:q是整数,且数列
).求证:q是整数,且数列![]() 中的任意一项都是数列
中的任意一项都是数列![]() 中的项.
中的项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正方形![]() 沿对角线
沿对角线![]() 折成直二面角,下列结论:①
折成直二面角,下列结论:①![]() 与
与![]() 所成的角为
所成的角为![]() :②
:②![]() 与
与![]() 所成的角为
所成的角为![]() :③
:③![]() 与面
与面![]() 所成角的正弦值为
所成角的正弦值为![]() :④二面角
:④二面角![]() 的平面角正切值是
的平面角正切值是![]() :其中正确结论的个数为( )
:其中正确结论的个数为( )
A.4B.3C.2D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 正方形
正方形![]() 所在平面,M是
所在平面,M是![]() 的中点,二面角
的中点,二面角![]() 的大小为
的大小为![]() .
.

(1)设l是平面![]() 与平面
与平面![]() 的交线,证明
的交线,证明![]() ;
;
(2)在棱![]() 是否存在一点N,使
是否存在一点N,使![]() 为
为![]() 的二面角.若不存在,说明理由:若存在,求
的二面角.若不存在,说明理由:若存在,求![]() 长.
长.
查看答案和解析>>
科目:高中数学 来源: 题型:
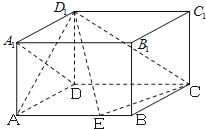
【题目】已知在长方体ABCD﹣A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
(Ⅰ)求证:D1E⊥A1D;
(Ⅱ)在棱AB上是否存在点E使得AD1与平面D1EC成的角为![]() ?若存在,求出AE的长,若不存在,说明理由.
?若存在,求出AE的长,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com