
【题目】已知各项都是正数的数列{an}的前n项和为Sn , Sn=an2+ ![]() an , n∈N*
an , n∈N*
(1)求数列{an}的通项公式;
(2)设数列{bn}满足:b1=1,bn﹣bn﹣1=2an(n≥2),求数列{ ![]() }的前n项和Tn
}的前n项和Tn
(3)若Tn≤λ(n+4)对任意n∈N*恒成立,求λ的取值范围.
【答案】
(1)解:∵Sn=an2+ ![]() an,
an,
∴Sn+1=an+12+ ![]() an+1,
an+1,
两式相减得:an+1= ![]() ﹣
﹣ ![]() +
+ ![]() (an+1﹣an),
(an+1﹣an),
∴(an+1+an)(an+1﹣an﹣ ![]() )=0,
)=0,
∵数列{an}的各项都是正数,
∴an+1﹣an= ![]() ,
,
又∵a1= ![]() +
+ ![]() a1,
a1,
∴a1= ![]() ,
,
∴数列{an}是以 ![]() 为首项、
为首项、 ![]() 为公差的等差数列,
为公差的等差数列,
∴an= ![]() +(n﹣1)
+(n﹣1) ![]() =
= ![]()
(2)解:∵an= ![]() ,
,
∴bn﹣bn﹣1=2an=2 ![]() =n,
=n,
∴b2﹣b1=2,
b3﹣b2=3,
…
bn﹣bn﹣1=n,
累加得:bn﹣b1= ![]() ,
,
又∵b1=1,
∴bn=b1+ ![]() =1+
=1+ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =2(
=2( ![]() ﹣
﹣ ![]() ),
),
∴ ![]()
(3)解:∵Tn= ![]() ,
,
∴Tn≤λ(n+4),
∴λ≥ ![]() =
= ![]() =
= ![]() ,
,
∵n+ ![]() ≥2
≥2 ![]() =4当且仅当n=2时取等号,
=4当且仅当n=2时取等号,
∴当n=2时 ![]() 有最大值
有最大值 ![]() ,
,
∴ ![]()
【解析】(1)通过Sn=an2+ ![]() an、Sn+1=an+12+
an、Sn+1=an+12+ ![]() an+1 , 作差、分析可得an+1﹣an=
an+1 , 作差、分析可得an+1﹣an= ![]() ,进而可得结论;(2)通过an=
,进而可得结论;(2)通过an= ![]() ,可得bn﹣bn﹣1=n,累加即得:bn﹣b1=
,可得bn﹣bn﹣1=n,累加即得:bn﹣b1= ![]() ,从而可得bn=
,从而可得bn= ![]() ,裂项可得
,裂项可得 ![]() =2(
=2( ![]() ﹣
﹣ ![]() ),并项相加即得结论;(3)通过Tn=
),并项相加即得结论;(3)通过Tn= ![]() 、Tn≤λ(n+4),整理可得λ≥
、Tn≤λ(n+4),整理可得λ≥ ![]() ,利用基本不等式即得结论.
,利用基本不等式即得结论.
【考点精析】认真审题,首先需要了解数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式).


科目:高中数学 来源: 题型:
【题目】下列命题中是真命题的是( )
①“若x2+y2≠0,则x,y不全为零”的否命题 ②“正多边形都相似”的逆命题
③“若m>0,则x2+x-m=0有实根”的逆否命题④“若x-![]() 是有理数,则x是
是有理数,则x是
无理数”的逆否命题
A、①②③④ B、①③④ C、②③④ D、①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O为坐标原点,椭圆C:![]() 的左、右焦点分别为F1,F2,右顶点为A,上顶点为B,若|OB|,|OF2|,|AB|成等比数列,椭圆C上的点到焦点F2的最短距离为
的左、右焦点分别为F1,F2,右顶点为A,上顶点为B,若|OB|,|OF2|,|AB|成等比数列,椭圆C上的点到焦点F2的最短距离为![]() .
.
(1)求椭圆C的标准方程;
(2)设T为直线x=-3上任意一点,过F1的直线交椭圆C于点P,Q,且![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“龟兔赛跑”讲述了这样的故事:领先的兔子看着慢慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点.用![]() ,
,![]() 分别表示乌龟和兔子所行的路程,
分别表示乌龟和兔子所行的路程,![]() 为时间,则与故事情节相吻合的是( )
为时间,则与故事情节相吻合的是( )
A.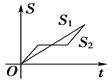 B.
B.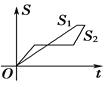 C.
C.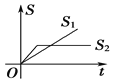 D.
D.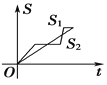
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=lnx﹣ ![]() ax2﹣bx
ax2﹣bx
(1)当a=b= ![]() 时,求函数f(x)的单调区间;
时,求函数f(x)的单调区间;
(2)当a=0,b=﹣1时,方程f(x)=mx在区间[1,e2]内有唯一实数解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() .
.
(1)判断函数f(x)的奇偶性;
(2)判断并用定义证明函数f(x)在其定义域上的单调性.
(3)若对任意的t![]() 1,不等式f(
1,不等式f(![]() )+f(
)+f(![]() )<0恒成立,求k的取值范围.
)<0恒成立,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com