
 ,
, ]
] ,得x2+y2+(1-x-y)2=
,得x2+y2+(1-x-y)2= ,整理成关于y的一元二次方程得:
,整理成关于y的一元二次方程得:  =0,∵y∈R,故Δ≥0
=0,∵y∈R,故Δ≥0 )≥0,得0≤x≤
)≥0,得0≤x≤ ,∴x∈[0,
,∴x∈[0, ]
] ]
] +x′,y=
+x′,y= +y′,z=
+y′,z= +z′,则x′+y′+z′=0,
+z′,则x′+y′+z′=0, =(
=( +x′)2+(
+x′)2+( +y′)2+(
+y′)2+( +z′)2
+z′)2 +x′2+y′2+z′2+
+x′2+y′2+z′2+ (x′+y′+z′)
(x′+y′+z′) +x′2+y′2+z′2≥
+x′2+y′2+z′2≥ +x′2+
+x′2+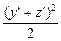 =
= +
+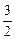 x′2
x′2 ,x′∈[-
,x′∈[- ,
, ],x∈[0,
],x∈[0, ],同理y,z∈[0,
],同理y,z∈[0, ]
] =x2+y2+z2≥x2+
=x2+y2+z2≥x2+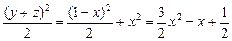 >
> ,矛盾
,矛盾
 ,不妨设x>
,不妨设x> ,
, =x2+y2+z2≥x2+
=x2+y2+z2≥x2+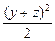 =x2+
=x2+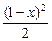 =
=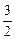 x2-x+
x2-x+
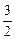 x(x-
x(x- )+
)+ >
>
 矛盾
矛盾
 ]
]

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案科目:高中数学 来源:不详 题型:单选题
 是定义在正整数集上的函数,且
是定义在正整数集上的函数,且 满足:“当
满足:“当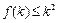 成立时,总可推出
成立时,总可推出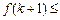
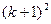 成立”.那么,下列命题总成立的是
成立”.那么,下列命题总成立的是A.若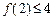 成立,则当 成立,则当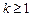 时,均有 时,均有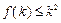 成立 成立 |
B.若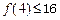 成立,则当 成立,则当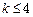 时,均有 时,均有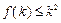 成立 成立 |
C.若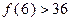 成立,则当 成立,则当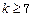 时,均有 时,均有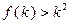 成立 成立 |
D.若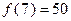 成立,则当 成立,则当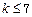 时,均有 时,均有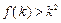 成立 成立 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com