
【题目】已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,圆
轴正半轴为极轴,建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和圆
的普通方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 是直线
是直线![]() 上的动点,过
上的动点,过![]() 作直线与圆
作直线与圆![]() 相切,切点分别为
相切,切点分别为![]() 、
、![]() ,若使四边形
,若使四边形![]() 的面积最小,求此时点
的面积最小,求此时点![]() 的坐标.
的坐标.
【答案】(1)![]() ,
,![]() (2)点
(2)点![]() 的坐标为
的坐标为![]() .
.
【解析】分析:(1)利用代入法消去参数可得直线![]() 的普通方程,将圆的极坐标方程,利用两角差的余弦公式展开,两边同乘
的普通方程,将圆的极坐标方程,利用两角差的余弦公式展开,两边同乘![]() ,根据互化公式可得圆
,根据互化公式可得圆![]() 的直角坐标方程;(2)若使四边形
的直角坐标方程;(2)若使四边形![]() 的面积最小,则
的面积最小,则![]() 的面积要最小,要使
的面积要最小,要使![]() 的面积要最小,只需
的面积要最小,只需![]() 最小即可,若
最小即可,若![]() 最小,则
最小,则![]() 最小,当
最小,当![]() 最小时,
最小时,![]() ,进而可得结果.
,进而可得结果.
详解:(1)直线![]() 的参数方程为
的参数方程为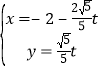 (
(![]() 为参数),
为参数),
消去参数![]() 得直线
得直线![]() 的普通方程为
的普通方程为![]() .
.
由![]()
![]() ,
,
两边同乘![]() 得,
得,![]() ,
,
∴![]() ,
,
∴圆![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(2)依题意,若使四边形![]() 的面积最小,则
的面积最小,则![]() 的面积要最小,
的面积要最小,
由![]() ,其中
,其中![]() 等于圆
等于圆![]() 的半径
的半径![]() ,
,
∴要使![]() 的面积要最小,只需
的面积要最小,只需![]() 最小即可,
最小即可,
又![]() ,
,
∴若![]() 最小,则
最小,则![]() 最小,
最小,
又点![]() 为圆心,点
为圆心,点![]() 是直线
是直线![]() 上动点,∴当
上动点,∴当![]() 最小时,
最小时,![]() ,
,
设![]() ,
,
∴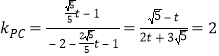 ,解得
,解得![]() ,
,
∴当四边形![]() 的面积最小时,点
的面积最小时,点![]() 的坐标为
的坐标为![]() .
.


科目:高中数学 来源: 题型:
【题目】从某小区抽取100户居民进行月用电量调查,发现其用电量都在50度至350度之间,频率分布直方图如图所示. 
(1)根据直方图求x的值,并估计该小区100户居民的月均用电量(同一组中的数据用该组区间的中点值作代表);
(2)从该小区已抽取的100户居民中,随机抽取月用电量超过250度的3户,参加节约用电知识普及讲座,其中恰有ξ户月用电量超过300度,求ξ的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据某市供电公司数据,2019年1月份市新能源汽车充电量约270万度,同比2018年增长![]() ,为了增强新能源汽车的推广运用,政府加大了充电桩等基础设施的投入.现为了了解该城市充电桩等基础设施的使用情况,随机选取了200个驾驶新能源汽车的司机进行问卷调查,根据其满意度评分值(百分制)按照
,为了增强新能源汽车的推广运用,政府加大了充电桩等基础设施的投入.现为了了解该城市充电桩等基础设施的使用情况,随机选取了200个驾驶新能源汽车的司机进行问卷调查,根据其满意度评分值(百分制)按照![]() ,
,![]() ,…,
,…,![]() 分成5组,制成如图所示的频率分布直方图.
分成5组,制成如图所示的频率分布直方图.
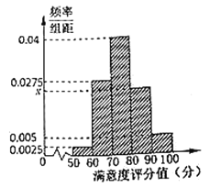
(1)求图中![]() 的值并估计样本数据的中位数;
的值并估计样本数据的中位数;
(2)已知满意度评分值在![]() 内的男女司机人数比为
内的男女司机人数比为![]() ,从中随机抽取2人进行座谈,求2人均为女司机的概率.
,从中随机抽取2人进行座谈,求2人均为女司机的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在(0,+∞)上的连续函数y=f(x)满足:xf′(x)﹣f(x)=xex且f(1)=﹣3,f(2)=0.则函数y=f(x)( )
A.有极小值,无极大值
B.有极大值,无极小值
C.既有极小值又有极大值
D.既无极小值又无极大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4﹣4:极坐标与参数方程
极坐标系与直角坐标系xOy有相同的长度单位,以原点O为极点,以x轴正半轴为极轴.已知曲线C1的极坐标方程为 ![]() ,曲线C2的极坐标方程为ρsinθ=a(a>0),射线
,曲线C2的极坐标方程为ρsinθ=a(a>0),射线 ![]() ,
, ![]() 与曲线C1分别交异于极点O的四点A,B,C,D.
与曲线C1分别交异于极点O的四点A,B,C,D.
(Ⅰ)若曲线C1关于曲线C2对称,求a的值,并把曲线C1和C2化成直角坐标方程;
(Ⅱ)求|OA||OC|+|OB||OD|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某工厂生产线上随机抽取16件零件,测量其内径数据从小到大依次排列如下(单位:![]() ):1.12,1.15,1.21,1.23,1.25,1.25,1.26,1.30,1.30,1.32,1.34,1.35,1.37,1.38,1.41,1.42,据此可估计该生产线上大约有25%的零件内径小于等于_____
):1.12,1.15,1.21,1.23,1.25,1.25,1.26,1.30,1.30,1.32,1.34,1.35,1.37,1.38,1.41,1.42,据此可估计该生产线上大约有25%的零件内径小于等于_____![]() ,大约有30%的零件内径大于_____
,大约有30%的零件内径大于_____![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() (a>b>0)的左、右焦点分别为F1 , F2 , 过F1且与x轴垂直的直线交椭圆于A、B两点,直线AF2与椭圆的另一个交点为C,若△ABF2的面积是△BCF2的面积的2倍,则椭圆的离心率为( )
(a>b>0)的左、右焦点分别为F1 , F2 , 过F1且与x轴垂直的直线交椭圆于A、B两点,直线AF2与椭圆的另一个交点为C,若△ABF2的面积是△BCF2的面积的2倍,则椭圆的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com