
【题目】若函数![]() 在区间
在区间![]() 上的最大值是
上的最大值是![]() ,最小值是
,最小值是![]() ,则
,则![]() ( )
( )
A.与![]() 有关,且与
有关,且与![]() 有关B.与
有关B.与![]() 有关,但与
有关,但与![]() 无关
无关
C.与![]() 无关,且与
无关,且与![]() 无关D.与
无关D.与![]() 无关,但与
无关,但与![]() 有关
有关
科目:高中数学 来源: 题型:
【题目】某调查机构几年前对全国互联网行业进行调查统计,得到整个互联网行业从业人员年龄分布扇形图、90后从事互联网行业岗位分布条形图,则下列结论中不一定正确的是( ).
注:90后指1990-1999年之间出生的人群,80后指1980-1989年之间出生的人群,80前指179年及以前出生的人群.
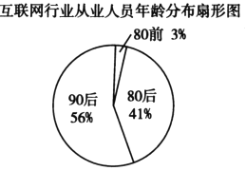

A.互联网行业从业人员中90后占一半以上
B.互联网行业中从事技术岗位的人数超过总人数的20%
C.互联网行业中从事运营岗位的人数90后比80前多
D.互联网行业中从事技术岗位的人数90后比80后多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】台风“山竹”导致海南省局部地方海啸,使当地的自来水受到了污染,某部门对水质监测后,决定往水中投放一种药剂来净化水质,已知每投放质量为![]() 的药剂后,经过
的药剂后,经过![]() 天该药剂在水中释放的浓度
天该药剂在水中释放的浓度![]() (毫克/升)满足
(毫克/升)满足![]() ,其中
,其中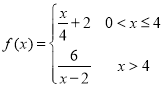 ,当药剂在水中释放的浓度不低于4(毫克/升)时称为有效净化,当药剂在水中释放的浓度不低于4(毫克/升)且不高于10(毫克/升)时称为最佳净化.
,当药剂在水中释放的浓度不低于4(毫克/升)时称为有效净化,当药剂在水中释放的浓度不低于4(毫克/升)且不高于10(毫克/升)时称为最佳净化.
(1)如果投放的药剂质量为![]() ,试问自来水达到有效净化一共可持续几天?
,试问自来水达到有效净化一共可持续几天?
(2)如果投放的药剂质量为![]() ,为了使在7天(从投放药剂算起包括第7天)之内的自来水达到最佳净化,试确定应该投放的药剂质量
,为了使在7天(从投放药剂算起包括第7天)之内的自来水达到最佳净化,试确定应该投放的药剂质量![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 位数满足下列条件:①各个数字只能从集合
位数满足下列条件:①各个数字只能从集合![]() 中选取;②若其中有数字4,则在4的前面不含2.将这样的n位数的个数记为
中选取;②若其中有数字4,则在4的前面不含2.将这样的n位数的个数记为![]()
(1)求![]() ;
;
(2)探究![]() 与
与![]() 之间的关系,求出数列
之间的关系,求出数列![]() 的通项公式;
的通项公式;
(3)对于每个正整数![]() ,在
,在![]() 与
与![]() 之间插入
之间插入![]() 个
个![]() 得到一个新数列
得到一个新数列![]() ,设
,设![]() 是数列
是数列![]() 的前
的前![]() 项和,试探究
项和,试探究![]() 能否成立?写出你探究得到的结论并给出证明.
能否成立?写出你探究得到的结论并给出证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com