
【题目】在锐角![]() 中,
中, ![]() 、
、![]() 、
、![]() 分别为角
分别为角![]() 、
、![]() 、
、![]() 所对的边,且
所对的边,且![]() .
.
(![]() )确定角
)确定角![]() 的大小.
的大小.
(![]() )若
)若![]() ,且
,且![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
【答案】(![]() )
)![]() ;(
;(![]() )
)![]()
【解析】试题分析:(1)由正弦定理可知, ![]() ,所以
,所以![]() ;(2)由题意,
;(2)由题意, ![]() ,
, ![]() ,得到
,得到![]() .
.
试题解析:
(![]() )
)![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() .
.
(![]() )
)![]() ,
, ![]() ,
,
![]() ,
,
∴![]() .
.
【题型】解答题
【结束】
17
【题目】已知等差数列![]() 满足:
满足:![]() ,
,![]() .
.![]() 的前n项和为
的前n项和为![]() .
.
(Ⅰ)求![]() 及
及![]() ;
;
(Ⅱ)若![]() ,
,![]() (
(![]() ),求数列
),求数列![]() 的前
的前![]() 项和
项和![]() .
.
科目:高中数学 来源: 题型:
【题目】某市公租房的房源位于甲、乙两个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,现该市有3位申请人在申请公租房:
(1)用合适的符号写出样本空间;
(2)求没有人申请甲片区房源的概率;
(3)求每个片区的房源都有人申请的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,学校决定利用随机数表法从中抽取100人进行成绩抽样调查.抽取的100人的数学与地理的水平测试成绩如下表:
人数 | 数学 | |||
优秀 | 良好 | 及格 | ||
地理 | 优秀 | 7 | 20 | 5 |
良好 | 9 | 18 | 6 | |
及格 | a | 4 | b | |
成绩分为优秀、良好、及格三个等级;横向,纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有20+18+4=42人.
(1)在该样本中,数学成绩优秀率是30%,求a,b的值;
(2)在地理成绩及格的学生中,已知a≥10,b≥7,求数学成绩优秀的人数比及格的人数少的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos2A﹣3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面积S=5![]() ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某公司2001年至2017年新产品研发费用![]() (单位:万元)的折线图.为了预测该公司2019年的新产品研发费用,建立了
(单位:万元)的折线图.为了预测该公司2019年的新产品研发费用,建立了![]() 与时间变量
与时间变量![]() 的两个线性回归模型.根据2001年至2017年的数据(时间变量
的两个线性回归模型.根据2001年至2017年的数据(时间变量![]() 的值依次为1,2,…,17)建立模型①:
的值依次为1,2,…,17)建立模型①:![]() ;根据2011年至2017年的数据(时间变量
;根据2011年至2017年的数据(时间变量![]() 的值依次为1,2,…,7)建立模型②:
的值依次为1,2,…,7)建立模型②:![]() .
.

(1)分别利用这两个模型,求该公司2019年的新产品研发费用的预测值;
(2)你认为用哪个模型得到的预测值更可靠?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市预测2000年到2004年人口总数与年份的关系如下表所示
年份200x(年) | 0 | 1 | 2 | 3 | 4 |
人口数y(十)万 | 5 | 7 | 8 | 11 | 19 |
(1)请根据上表提供的数据,计算![]() ,用最小二乘法求出
,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]()
(2) 据此估计2005年该城市人口总数。
(参考数值:0×5+1×7+2×8+3×11+4×19=132,![]()
参考公式:用最小二乘法求线性回归方程系数公式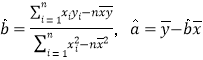 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com