本小题满分12分)
已知等差数列{
an}的首项
a1=1,公差
d>0,且
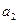
、

、
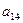
分别是一个等比数列的第二项、第三项、第四项.
(Ⅰ)求数列{
an}的通项公式;
(Ⅱ)设
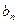
=

(
n∈N
*),

求

解:(Ⅰ)由题意得(
a1+
d)(
a1+

13
d)=(
a1+4
d)
2,整理得2
a1d=
d2.∵
a1=1,
解得(
d=0舍),
d=2. ∴
an=2
n-1(
n∈N
*).
(Ⅱ)
bn=
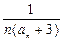
=
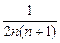
=

(

-
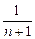
),∴
Sn=
b1+
b2+…+
bn=

[(1-

)+(

-

)+…+(

-
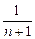
)]=

(1-
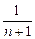
)=
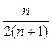
.
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:填空题
一个数分别加上20,50,100后得

到的三个数成等比数列,其公比为.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
若
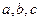
成等比数列,则函数
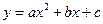
的图象与
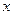
轴的交点的个数是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
等比数列
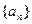
中,已知
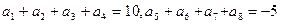
,则数列
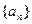
的前16项和S
16为( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
已知等比数列
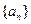
满足
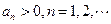
,且
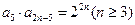
,则当
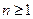
时,
 __________
__________
查看答案和解析>>

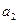 、
、 、
、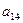 分别是一个等比数列的第二项、第三项、第四项.
分别是一个等比数列的第二项、第三项、第四项.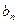 =
= (n∈N*),
(n∈N*), 求
求