
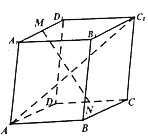
 已知平行六面体ABCD-A1B1C1D1,设A1D1中点为M,CD的中点为N,若∠A1AD=∠A1AB=∠BAD=60°且AA1=AB=AD=1,则|AC1|=$\sqrt{6}$,若$\overrightarrow{MN}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{A{A}_{1}}$,则x+y+z=0.
已知平行六面体ABCD-A1B1C1D1,设A1D1中点为M,CD的中点为N,若∠A1AD=∠A1AB=∠BAD=60°且AA1=AB=AD=1,则|AC1|=$\sqrt{6}$,若$\overrightarrow{MN}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{A{A}_{1}}$,则x+y+z=0. 分析 ①$\overrightarrow{A{C}_{1}}$=$\overrightarrow{AB}+\overrightarrow{AD}$+$\overrightarrow{A{A}_{1}}$,利用数量积运算性质可得${\overrightarrow{A{C}_{1}}}^{2}$=${\overrightarrow{AB}}^{2}+{\overrightarrow{AD}}^{2}$+${\overrightarrow{A{A}_{1}}}^{2}$+$2\overrightarrow{AB}•\overrightarrow{AD}$+2$\overrightarrow{AB}•\overrightarrow{A{A}_{1}}$+2$\overrightarrow{AD}•\overrightarrow{A{A}_{1}}$,即可得出.
②$\overrightarrow{MN}$=$\overrightarrow{AN}-\overrightarrow{AM}$=$\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AB}$-$(\overrightarrow{A{A}_{1}}+\frac{1}{2}\overrightarrow{AD})$=$\frac{1}{2}\overrightarrow{AB}$+$\frac{1}{2}\overrightarrow{AD}$-$\overrightarrow{A{A}_{1}}$,与$\overrightarrow{MN}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{A{A}_{1}}$比较即可得出.
解答 解:①$\overrightarrow{A{C}_{1}}$=$\overrightarrow{AB}+\overrightarrow{AD}$+$\overrightarrow{A{A}_{1}}$,
∴${\overrightarrow{A{C}_{1}}}^{2}$=${\overrightarrow{AB}}^{2}+{\overrightarrow{AD}}^{2}$+${\overrightarrow{A{A}_{1}}}^{2}$+$2\overrightarrow{AB}•\overrightarrow{AD}$+2$\overrightarrow{AB}•\overrightarrow{A{A}_{1}}$+2$\overrightarrow{AD}•\overrightarrow{A{A}_{1}}$=3+2×3×cos60°=6,
解得$|\overrightarrow{A{C}_{1}}|$=$\sqrt{6}$.
②$\overrightarrow{MN}$=$\overrightarrow{AN}-\overrightarrow{AM}$=$\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AB}$-$(\overrightarrow{A{A}_{1}}+\frac{1}{2}\overrightarrow{AD})$=$\frac{1}{2}\overrightarrow{AB}$+$\frac{1}{2}\overrightarrow{AD}$-$\overrightarrow{A{A}_{1}}$,
与$\overrightarrow{MN}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{A{A}_{1}}$比较可得:x=$\frac{1}{2}$=y,z=-1.
则x+y+z=0.
故答案为:$\sqrt{6}$,0.
点评 本题考查了向量三角形法则、平行四边形法则、平面向量基本定理、向量共线定理、数量积运算性质,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
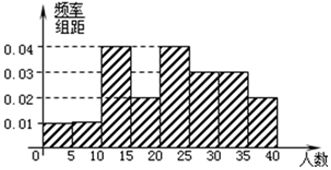
| A. | 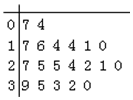 | B. | 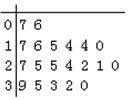 | C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-5,5) | B. | (5,-5) | C. | (-3,3) | D. | (3,-3) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com