
【题目】已知正项数列![]() 满足:
满足: ![]() ,
, ![]() .
.![]() 为数列
为数列![]() 的前
的前![]() 项和.
项和.
(Ⅰ)求证:对任意正整数![]() ,有
,有![]() ;
;
(Ⅱ)设数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:对任意
,求证:对任意![]() ,总存在正整数
,总存在正整数![]() ,使得
,使得![]() 时,
时, ![]() .
.
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+bx+c满足f(2﹣x)=f(2+x),f(0)>0,且f(m)=f(n)=0(m≠n),则log4m﹣ ![]() n的值是( )
n的值是( )
A.小于1
B.等于1
C.大于1
D.由b的符号确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】广播电台为了了解某地区的听众对某个戏曲节目的收听情况,随机抽取了100名听众进行调查,下面是根据调查结果绘制的听众日均收听该节目的频率分布直方图,将日均收听该节目时间不低于40分钟的听众成为“戏迷” 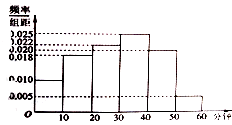
(1)根据已知条件完成2×2列联表,并判断“戏迷”与性别是否有关?
“戏迷” | 非戏迷 | 总计 | |
男 | |||
女 | 10 | 55 | |
总计 |
附:K2= ![]() ,
,
P(K2≥k) | 0.05 | 0.01 |
k | 3.841 | 6.635 |
(2)将上述调查所得到的频率当作概率.现在从该地区大量的听众中,采用随机抽样的方法每次抽取1名听众,抽取3次,记被抽取的3名听众中“戏迷”的人数为X,若每次抽取的结果相互独立,求X的分布列,数学期望及方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系xOy中,曲线C:(x﹣1)2+y2=1.直线l经过点P(m,0),且倾斜角为 ![]() .以O为极点,以x轴正半轴为极轴,建立坐标系.
.以O为极点,以x轴正半轴为极轴,建立坐标系.
(1)写出曲线C的极坐标方程与直线l的参数方程;
(2)若直线l与曲线C相交于A,B两点,且|PA||PB|=1,求实数m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com