
����Ŀ��ij��ѧ���ѡȡ��![]() �������������ǵ�������Ϊ��������ͳ�ƣ��õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ���۲�ͼ�����ݣ�����������⣮
�������������ǵ�������Ϊ��������ͳ�ƣ��õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ���۲�ͼ�����ݣ�����������⣮
��![]() ����
����![]() ��ֵ������������������
��ֵ������������������![]() ����λ��
�����![]() ����������
����������
��![]() ��������һ���е�ÿ�����ݿ��ø���������е�ֵ���棬ͨ���������Ƹ�Уȫ��������ƽ�����ߣ�
��������һ���е�ÿ�����ݿ��ø���������е�ֵ���棬ͨ���������Ƹ�Уȫ��������ƽ�����ߣ�
��![]() ������������������
������������������![]() ��
��![]() �����
����λ��![]() ���ڵ���������ѡ���ˣ��������˵����߶�������
���ڵ���������ѡ���ˣ��������˵����߶�������![]() �ĸ��ʣ�
�ĸ��ʣ�
���𰸡���1��4����2��0.4
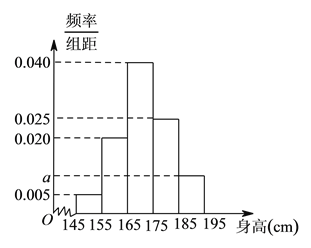
�������������������![]() �������⣬����Ƶ�ʷֲ�ֱ��ͼ�������ε����֮��Ϊ
�������⣬����Ƶ�ʷֲ�ֱ��ͼ�������ε����֮��Ϊ![]() ���������
���������![]() ��ֵ�������õ�������
��ֵ�������õ�������![]() ��Ƶ�ʺ�����Ϊ��
��Ƶ�ʺ�����Ϊ��
��![]() ������ƽ�����ļ��㹫ʽ���������ȫУ������ƽ�����ߣ�
������ƽ�����ļ��㹫ʽ���������ȫУ������ƽ�����ߣ�
��![]() ������Ƶ�ʷֲ�ֱ��ͼ���ɵ�������
������Ƶ�ʷֲ�ֱ��ͼ���ɵ�������![]() ��
��![]() �ڵ������������������ùŵ���͵ĸ��ʼ��㹫ʽ�����������Ӧ�ĸ���.
�ڵ������������������ùŵ���͵ĸ��ʼ��㹫ʽ�����������Ӧ�ĸ���.
���������
��![]() �������⣺
�������⣺![]() ��
��
������![]() ��Ƶ��Ϊ
��Ƶ��Ϊ![]() ������Ϊ
������Ϊ![]() ��
��
��![]() �����������������ߵ�ƽ��ֵΪ
�����������������ߵ�ƽ��ֵΪ![]() ����
����
![]()
![]() ��
��
���ԣ����Ƹ�Уȫ��������ƽ������Ϊ![]() ��
��
��![]() ����������������
����������������![]() ��
��![]() �����
����λ��![]() ���ڵ������ֱ���
���ڵ������ֱ���![]() �ˣ�
�ˣ�![]() �ˣ���������
�ˣ���������![]() ��
��![]() �����
����λ��![]() ���ڵ���������ѡ���ˣ���
���ڵ���������ѡ���ˣ���![]() �֣������˵����߶�������
�֣������˵����߶�������![]() ����
����![]() �֣������������Ϊ
�֣������������Ϊ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����塰����������ln+x= ![]() �������ĸ����⣺ ����a��0��b��0����ln+��ab��=bln+a
�������ĸ����⣺ ����a��0��b��0����ln+��ab��=bln+a
����a��0��b��0����ln+��ab��=ln+a+ln+b
����a��0��b��0���� ![]() b
b
����a��0��b��0����ln+��a+b����ln+a+ln+b+ln2
���е��������У� �� ��д������������ı�ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУΪ���˽����ѧ��ÿ������ѧϰ�й��ŵ���ѧ��ʱ�䣬�����ȡ�˸���������Ů����50�������ʾ����飬����ÿ������ѧϰ�й��ŵ���ѧ��ʱ�䳬��3Сʱ��ѧ����Ϊ�������ԡ�������Ϊ���ǹ����ԡ��������������
������ | �ǹ����� | �ϼ� | |
���� | 26 | 24 | 50 |
�� | 30 | 20 | 50 |
�ϼ� | 56 | 44 | 100 |
�����ݱ��������ܷ��ж���60%�İ�����Ϊ�������ԡ����Ա��йأ�
�����ִӵ����Ů���а��ֲ�����ķ������5�˽��е��飬������ȡ��5���С������ԡ��͡��ǹ����ԡ���������
�����ִӣ���������ȡ��5�����������ȡ3�˽��е��飬����3���С������ԡ�������Ϊ�Σ�����������εķֲ�������ѧ������
�ο���ʽ��K2= ![]() ������n=a+b+c+d��
������n=a+b+c+d��
�ο����ݣ�
P��K2��k0�� | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
k0 | 0.455 | 0.708 | 1.321 | 3.841 | 5.024 | 6.635 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��2x2+x��y��n��չ��ʽ�и���ϵ���ĺ�Ϊ32����չ��ʽ��x5y2��ϵ��Ϊ �� ������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���о����ýγ��ڸ��ٹ�·�ϵij����������ͨ���������50�����ýγ���ʻԱ���е��飬�õ����ڸ��ٹ�·����ʻʱ��ƽ���������Ϊ����30�����Լ�ʻԱ�У�ƽ�����ٳ���100km/h����20�ˣ�������100km/h����10�ˣ���20��Ů�Լ�ʻԱ�У�ƽ�����ٳ���100km/h����5�ˣ�������100km/h����15�ˣ�
�����������������������ж��Ƿ���99.5%�İ�����Ϊƽ�����ٳ���100km/h�������Ա��йأ�
ƽ�����ٳ���100km/h���� | ƽ�����ٲ�����100km/h���� | �ϼ� | |
���Լ�ʻԱ���� | |||
Ů�Լ�ʻԱ���� | |||
�ϼ� | |||
���������������������������壬�ִӸ��ٹ�·����ʻ�Ĵ������ýγ��������ȡ3��������3�����м�ʻԱΪŮ���ҳ��ٲ�����100km/h�ij�����Ϊ�ƣ���ÿ�γ�ȡ�Ľ����������ģ���Ƶķֲ��к���ѧ������
�ο���ʽ�� ![]() ������n=a+b+c+d��
������n=a+b+c+d��
�ο����ݣ�
P��K2��k0�� | 0.150 | 0.100 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����������г齱����ٰ췽�����˼ס������ֳ齱�������������н���Ϊ ![]() ���н����Ի��2�֣������ҵ��н���Ϊ
���н����Ի��2�֣������ҵ��н���Ϊ ![]() ���н����Ի��3�֣�δ�н��÷֣�ÿ������ֻ��һ�γ齱���ᣬÿ�γ齱�н����Ӱ�죬���������ƾ�����һ���Ʒ��
���н����Ի��3�֣�δ�н��÷֣�ÿ������ֻ��һ�γ齱���ᣬÿ�γ齱�н����Ӱ�죬���������ƾ�����һ���Ʒ��
��1����С��ѡ���׳齱��С��ѡ���ҳ齱�������ǵ��ۼƵ÷�Ϊx����x��3�ĸ��ʣ�
��2����С����С�����˶�ѡ����ѡ���ҽ��г齱���ʣ�����ѡ����ַ����齱���ۼƵ÷ֵ���ѧ�����ϴ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������C1�� ![]() ��
�� ![]() =1��a��0��b��0������F1������C2��x2+y2=a2�����ߣ����е�ΪM���ӳ�F1M������C3��y2=2px��p��0���ڵ�N����������C1��C3��һ����ͬ�Ľ��㣬��|MF1|=|MN|��������C1��������Ϊ�� ��
=1��a��0��b��0������F1������C2��x2+y2=a2�����ߣ����е�ΪM���ӳ�F1M������C3��y2=2px��p��0���ڵ�N����������C1��C3��һ����ͬ�Ľ��㣬��|MF1|=|MN|��������C1��������Ϊ�� ��
A.![]()
B.![]() ��1
��1
C.![]() +1
+1
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲��±���
1��
2��3��
4��5��6��7��
8��9��10��11��12��13��14��15��
����
�ʣ���1���˱���n�еĵ�һ���������һ�����ֱ��Ƕ��٣�
��2���˱���n�еĸ�����֮���Ƕ��٣�
��3��2012�ǵڼ��еĵڼ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������A={1��2��3}��B={��x��y��|x+y��4��0��x��y��A}����B�е�Ԫ�ظ���Ϊ�� ��
A.9
B.6
C.4
D.3
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com