
【题目】已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,﹣ ![]() <φ<0)的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x0 , 2)和(x0+2π,﹣2).
<φ<0)的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x0 , 2)和(x0+2π,﹣2).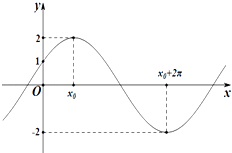
(1)求函数f(x)的解析式;
(2)若锐角θ满足f(2θ+ ![]() )=
)= ![]() ,求f(2θ)的值.
,求f(2θ)的值.
科目:高中数学 来源: 题型:
【题目】已知数列{an}与{bn}满足an+1﹣an=2(bn+1﹣bn),n∈N+ , bn=2n﹣1,且a1=2.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设 ![]() ,Tn为数列{cn}的前n项和,求Tn .
,Tn为数列{cn}的前n项和,求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,
, ![]() .
.
(1)求函数f(x)的值域;
(2)已知锐角△ABC的两边长a,b分别为函数f(x)的最小值与最大值,且△ABC的外接圆半径为 ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记等差数列{an}的前n项和为Sn .
(1)求证:数列{ ![]() }是等差数列;
}是等差数列;
(2)若a1=1,对任意的n∈N*,n≥2,均有 ![]() ,
, ![]() ,
, ![]() 是公差为1的等差数列,求使
是公差为1的等差数列,求使 ![]() 为整数的正整数k的取值集合;
为整数的正整数k的取值集合;
(3)记bn=a ![]() (a>0),求证:
(a>0),求证: ![]() ≤
≤ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}是各项均为正数的等比数列,其前n项和为Sn , 且a1a5=64,S5﹣S3=48.
(1)求数列{an}的通项公式;
(2)设有正整数m,l(5<m<l),使得am , 5a5 , al成等差数列,求m,l的值;
(3)设k,m,l∈N*,k<m<1,对于给定的k,求三个数 5ak , am , al经适当排序后能构成等差数列的充要条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx+x2 .
(Ⅰ)若函数g(x)=f(x)﹣ax在其定义域内为增函数,求实数a的取值范围;
(Ⅱ)在(Ⅰ)的条件下,若a>1,h(x)=e3x﹣3aexx∈[0,ln2],求h(x)的极小值;
(Ⅲ)设F(x)=2f(x)﹣3x2﹣kx(k∈R),若函数F(x)存在两个零点m,n(0<m<n),且2x0=m+n.问:函数F(x)在点(x0 , F(x0))处的切线能否平行于x轴?若能,求出该切线方程;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,角A,B,C所对的边分别为a,b,c,且3bsinA=c,D为AC边上一点.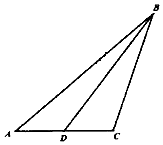
(1)若D是AC的中点,且 ![]() ,
, ![]() ,求△ABC的最短边的边长.
,求△ABC的最短边的边长.
(2)若c=2b=4,S△BCD= ![]() ,求DC的长.
,求DC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司对应聘人员进行能力测试,测试成绩总分为150分.下面是30位应聘人员的测试成绩的测试成绩:64,116,82,93,102,82,104,67,93,118,70,95,119,106,83,72,95,106,72,119,122,95,86,74,131,76,88,108,97,123.
(1)求应聘人员的测试成绩的样本平均数 ![]() (保留小数点后两位);
(保留小数点后两位);
(2)根据以上数据完成下面茎叶图:
应聘人员的测试成绩 | |
6 | |
7 | |
8 | |
9 | |
10 | |
11 | |
12 | |
13 | |
(3)由茎叶图可以认为,应聘人员的测试成绩Z服从正态分布N(μ,σ2),其中μ近似为样本平均数 ![]() ,σ2近似为样本方差s2 , 其中s2=18.872 , 利用该正态分布,求P(76.40<Z<114.14).
,σ2近似为样本方差s2 , 其中s2=18.872 , 利用该正态分布,求P(76.40<Z<114.14).
附:若Z~N(μ,σ2),则P(μ﹣σ<Z<μ+σ)=0.6826,
P(μ﹣2σ<Z<μ+2σ)=0.9544.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com