
分析 设sinA=m,sinB=n,由正弦定理和余弦定理分析出cosC有唯一确定值的方法.
解答 解:设sinA=m,sinB=n,由正弦定理$\frac{sinA}{a}=\frac{sinB}{b}=\frac{sinC}{c}=k$,得到a=$\frac{sinA}{k}$=$\frac{m}{k}$,b=$\frac{4}{5k}$=$\frac{n}{k}$,c=$\frac{sinC}{k}$,
又由余弦定理得到cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{{m}^{2}+{n}^{2}-1+co{s}^{2}C}{2mn}$,所以cos2C-2mncosC+(m2+n2-1)=0,
因为cosC具有唯一确定的值,所以判别式△=4m2n2-4(m2+n2-1)=0,
化简得(m2-1)(n2-1)=0,由于m,n不能同时为1,所以m,n只有一个为1时,即三角形为直角三角形时,cosC有唯一确定的值;此时A=0;
故答案为:0.
点评 本题考查了正弦定理和余弦定理的运用;从方程判别式的角度求出cosC有唯一确定值的方法.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 双曲线 | B. | 抛物线 | C. | 两条相交直线 | D. | 椭圆 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
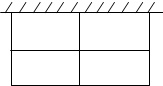 如图,动物园要围成相同面积的长方形虎笼四间,一面可利用原有的墙,其他各面用钢筋网围成.现有可围36m长网的材料,每间虎笼的长、宽各设计为多少时,可使每间虎笼的面积最大?
如图,动物园要围成相同面积的长方形虎笼四间,一面可利用原有的墙,其他各面用钢筋网围成.现有可围36m长网的材料,每间虎笼的长、宽各设计为多少时,可使每间虎笼的面积最大?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {x|-3≤x<-1,或x>1} | C. | {x|-3≤x≤-1,或x≥1} | D. | {x|x>1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{7}}{4}$ | B. | $\frac{4}{5}$ | C. | ±$\frac{\sqrt{7}}{4}$ | D. | ±$\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com