②③⑤
分析:根据正弦函数的图象与性质,通过举反例得到①不正确;根据向量数量积的性质,得到②正确;根据对数函数的图象特征,结合函数图象平移的规律,得到③正确;用辅助角公式化简,结合正余弦函数的奇偶性,得到④不正确;根据一元二次不等式解集的结论,可得⑤正确.由此得到正确答案.
解答:对于①,因为x>0时,sin|x|=sinx,此时不满足f(x+π)≠f(x),故①是假命题;
对于②,因为向量
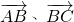
的夹角是角B的补角,所以
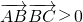
时,π-B是锐角,
故B为钝角,△ABC是钝角三角形,故②是真命题;
对于③,因为y=log
ax图象经过点(1,0),而函数y=2+log
a(x-2)图象是由y=log
ax右移2个单位,再上移2个单位而得,故y=2+log
a(x-2)图象必经过点(3,2),因此③是真命题;
对于④,y=cosx-sinx=

cos(x+

),所以y=cosx-sinx的图象向左平移

个单位,得到的解析式为y=

cos(x+

)=-

sinx,图象不关于y轴对称,故④是假命题;
对于⑤,命题“?x∈R,x
2+x+a<0”是假命题,说明x
2+x+a的最小值a-

≥0,可得a≥

,因此⑤是真命题
综上所述,正确命题的序号为:②③⑤
故答案为:②③⑤
点评:本题以命题真假的判断为载体,着重考查了函数的周期性、三角函数的奇偶性和向量数量积的性质等知识,属于基础题.准确理解相关的概念对各个选项加以正确判断,是解决本题的关键.

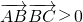 ,则△ABC一定是钝角三角形;
,则△ABC一定是钝角三角形; 个单位,所得图象关于y轴对称;
个单位,所得图象关于y轴对称;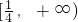 ;
;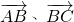 的夹角是角B的补角,所以
的夹角是角B的补角,所以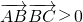 时,π-B是锐角,
时,π-B是锐角, cos(x+
cos(x+ ),所以y=cosx-sinx的图象向左平移
),所以y=cosx-sinx的图象向左平移 个单位,得到的解析式为y=
个单位,得到的解析式为y= cos(x+
cos(x+ )=-
)=- sinx,图象不关于y轴对称,故④是假命题;
sinx,图象不关于y轴对称,故④是假命题; ≥0,可得a≥
≥0,可得a≥ ,因此⑤是真命题
,因此⑤是真命题

 阅读快车系列答案
阅读快车系列答案