
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),圆
为参数),圆![]() 与圆
与圆![]() 外切于原点
外切于原点![]() ,且两圆圆心的距离
,且两圆圆心的距离![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求圆![]() 和圆
和圆![]() 的极坐标方程;
的极坐标方程;
(2)过点![]() 的直线
的直线![]() 、
、![]() 与圆
与圆![]() 异于点
异于点![]() 的交点分别为点
的交点分别为点![]() 和点
和点![]() ,与圆
,与圆![]() 异于点
异于点![]() 的交点分别为点
的交点分别为点![]() 和点
和点![]() ,且
,且![]() .求四边形
.求四边形![]() 面积的最大值.
面积的最大值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】【2018湖南(长郡中学、株洲市第二中学)、江西(九江一中)等十四校高三第一次联考】已知函数![]() (其中
(其中![]() 且
且![]() 为常数,
为常数, ![]() 为自然对数的底数,
为自然对数的底数, ![]() ).
).
(Ⅰ)若函数![]() 的极值点只有一个,求实数
的极值点只有一个,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)当![]() 时,若
时,若![]() (其中
(其中![]() )恒成立,求
)恒成立,求![]() 的最小值
的最小值![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 平面ABCD,四边形ABCD是正方形,PA=AD=2,点E、F、G分别为线段PA、PD和CD的中点.
平面ABCD,四边形ABCD是正方形,PA=AD=2,点E、F、G分别为线段PA、PD和CD的中点.
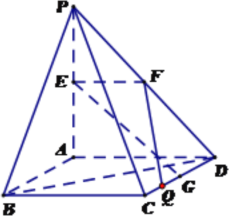
(1)求异面直线EG与BD所成角的大小;
(2)在线段CD上是否存在一点Q,使得点A到平面EFQ的距离恰为![]() ?若存在,求出线段CQ的长;若不存在,请说明理由.
?若存在,求出线段CQ的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,摩天轮的半径为40m,其中心![]() 点距离地面的高度为50m,摩天轮按逆时针方向做匀速转动,且20min转一圈,若摩天轮上点
点距离地面的高度为50m,摩天轮按逆时针方向做匀速转动,且20min转一圈,若摩天轮上点![]() 的起始位置在最高点处,则摩天轮转动过程中( )
的起始位置在最高点处,则摩天轮转动过程中( )

A.经过10min点![]() 距离地面10m
距离地面10m
B.若摩天轮转速减半,则其周期变为原来的![]() 倍
倍
C.第17min和第43min时![]() 点距离地面的高度相同
点距离地面的高度相同
D.摩天轮转动一圈,![]() 点距离地面的高度不低于70m的时间为
点距离地面的高度不低于70m的时间为![]() min
min
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】科技创新在经济发展中的作用日益凸显.某科技公司为实现9000万元的投资收益目标,准备制定一个激励研发人员的奖励方案:当投资收益达到3000万元时,按投资收益进行奖励,要求奖金![]() (单位:万元)随投资收益
(单位:万元)随投资收益![]() (单位:万元)的增加而增加,奖金总数不低于100万元,且奖金总数不超过投资收益的20%.
(单位:万元)的增加而增加,奖金总数不低于100万元,且奖金总数不超过投资收益的20%.
(1)现有三个奖励函数模型:①![]() ,②
,②![]() ,③
,③![]() ,
,![]() .试分析这三个函数模型是否符合公司要求?
.试分析这三个函数模型是否符合公司要求?
(2)根据(1)中符合公司要求的函数模型,要使奖金额达到350万元,公司的投资收益至少要达到多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是
A. 相关关系是一种非确定性关系
B. 线性回归方程对应的直线![]() ,至少经过其样本数据点
,至少经过其样本数据点![]() 中的一个点
中的一个点
C. 在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高
D. 在回归分析中,![]() 为
为![]() 的模型比
的模型比![]() 为
为![]() 的模型拟合的效果好
的模型拟合的效果好
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某超市,随机调查了100名顾客购物时使用手机支付的情况,得到如下的![]() 列联表,已知其中从使用手机支付的人群中随机抽取1人,抽到青年的概率为
列联表,已知其中从使用手机支付的人群中随机抽取1人,抽到青年的概率为![]() .
.
(1)根据已知条件完成![]() 列联表,并根据此资料判断是否有
列联表,并根据此资料判断是否有![]() 的把握认为“超市购物用手机支付与年龄有关”?
的把握认为“超市购物用手机支付与年龄有关”?
(2)现采用分层抽样从这100名顾客中按照“使用手机支付”和“不使用手机支付”中抽取得到一个容量为5的样本,设事件![]() 为“从这个样本中任选3人,这3人中至少有2人是使用手机支付的”,求事件
为“从这个样本中任选3人,这3人中至少有2人是使用手机支付的”,求事件![]() 发生的概率?
发生的概率?
![]() 列联表
列联表
青年 | 中老年 | 合计 | |
使用手机支付 | 60 | ||
不使用手机支付 | 28 | ||
合计 | 100 |
|
|
|
|
| 0.001 |
|
|
|
|
| 10.828 |
附:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个棱长为![]() 的正方体的表面涂上颜色,将其适当分割成棱长为
的正方体的表面涂上颜色,将其适当分割成棱长为![]() 的小正方体,全部放入不透明的口袋中,搅拌均匀后,从中任取一个,取出的小正方体表面仅有一个面涂有颜色的概率是()
的小正方体,全部放入不透明的口袋中,搅拌均匀后,从中任取一个,取出的小正方体表面仅有一个面涂有颜色的概率是()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com