练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．如图，直线y=x-2与圆x2+y2-4x+3=0及抛物线y2=8x依次交于A、B、C、D四点，则|AB|+|CD|=（　　）
    A．13B．14C．15D．16

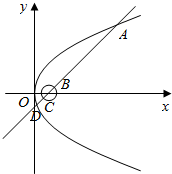
    分析 化圆的方程为（x-2）2+y2=1，抛物线y2=8x的焦点为（2，0），直线y=x-2过（2，0）点，则|AB|+|CD|=|AD|-2，联立直线y=x-2与y2=8x可得x2-12x+4=0，由此能够推导出|AB|+|CD|=16-2=14．

    解答 解：由x2+y2-4x+3=0，得（x-2）2+y2=1，
    ∵抛物线y2=8x的焦点为（2，0），∴直线y=x-2过（2，0）点，
    则|AB|+|CD|=|AD|-2，
    联立直线y=x-2与y2=8x，可得x2-12x+4=0，
    设A（x1，y1），D（x2，y2），则x1+x2=12，
    则有|AD|=（x1+x2）+4=16，
    故|AB|+|CD|=16-2=14．
    故选：B．

    点评 本题考查圆锥曲线和直线 的综合运用，解题时要注意合理地进行等价转化，是中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    10．（1）若f（x）+f（$\frac{x-1}{x}$）=1+x，求f（x）；
    （2）若2f（x）+f（1-x）=1+x，求f（x）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知指数函数y=ax（a＞0，且a≠1）的图象经过点（1，3）．
    （1）求函数的解析式；
    （2）求当x=-1，0，2时的函数值；
    （3）画出函数的图象；
    （4）叙述函数的性质．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知数列{an}的首项a1=1，?n∈N*，an+1=$\frac{2{a}_{n}}{2+{a}_{n}}$．
    （1）求数列{an}的通项公式；
    （2）求数列{$\frac{{a}_{n}}{n}$}的前n项和Sn；
    （3）求证：?n∈N*，a12+a22+a32+…+an2＜3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．已知集合M={x|（x-a）（x2-ax+a-1）=0}中各元素之和为3，则实数a的值为2或$\frac{3}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知两个大小相等的共点力F1，F2，当他们的夹角为90°时，合力的大小为10N，则当他们的夹角是120°时，合力大小是$5\sqrt{2}$N．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．某工厂生产某种产品，固定成本20000元，每生产一件产品成本增加100元，已知总收益R元（R指工厂售出产品的全部收入，它是成本与利润之和），是年产量Q（单位：件）的函数．满足关系式$R=\left\{\begin{array}{l}400Q-\frac{1}{2}{Q^2}\;\;\;（0≤Q≤400）\\ 80000\;\;\;\;\;\;\;\;\;\;\;\;\;\;（Q＞400）\end{array}\right.$，求该厂每年生产多少件产品，总利润最大，最大值是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知在△ABC中，sinA+cosA=$\frac{{\sqrt{5}}}{5}$
    （Ⅰ）求sinA-cosA的值；
    （Ⅱ）求$\frac{{5{{sin}^2}A+sin（A-\frac{π}{2}）cos（A+\frac{3π}{2}）-5{{cos}^2}A}}{sinAcosA}$的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．已知非零向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}-\overrightarrow{b}$|，＜$\overrightarrow{c}-\overrightarrow{a}，\overrightarrow{c}-\overrightarrow{b}$＞=$\frac{2π}{3}$，则$\frac{|\overrightarrow{c}|}{|\overrightarrow{a}|}$的最大值为$\frac{2\sqrt{3}}{3}$．

    查看答案和解析>>

    同步练习册答案