
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) | [110,120) | [120,130) | [130,140) | [140,150) |
| 频数 | 2 | 3 | 10 | 15 | 15 | x | 3 | 1 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) | [110,120) | [120,130) | [130,140) | [140,150) |
| 频数 | 1 | 2 | 9 | 8 | 10 | 10 | y | 3 |
| 甲校 | 乙校 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
 ),写出变量的概率,做出变量的分布列,再求出变量的期望值.
),写出变量的概率,做出变量的分布列,再求出变量的期望值.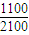 =55人成绩,乙校抽取了105-55=50人成绩
=55人成绩,乙校抽取了105-55=50人成绩| 甲校 | 乙校 | 总计 | |
| 优秀 | 10 | 20 | 30 |
| 非优秀 | 45 | 30 | 75 |
| 总计 | 55 | 50 | 105 |
 ≈6.109<6.635,
≈6.109<6.635, ,ξ的可能取值为0,1,2,3.
,ξ的可能取值为0,1,2,3. ),且P(ξ=k)=C
),且P(ξ=k)=C (
(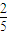 )k(
)k( )3-k,(k=0,1,2,3)
)3-k,(k=0,1,2,3)
 =
=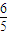 .
.

 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) | [110,120) | [120,130) | [130,140) | [140,150) |
| 频数 | 2 | 3 | 10 | 15 | 15 | x | 3 | 1 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) | [110,120) | [120,130) | [130,140) | [140,150) |
| 频数 | 1 | 2 | 9 | 8 | 10 | 10 | y | 3 |
| 甲校 | 乙校 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) | [110,120) | [120,130) | [130,140) | [140,150) |
| 频数 | 2 | 3 | 10 | 15 | 15 | x | 3 | 1 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) | [110,120) | [120,130) | [130,140) | [140,150) |
| 频数 | 1 | 2 | 9 | 8 | 10 | 10 | y | 3 |
| 甲校 | 乙校 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
查看答案和解析>>
科目:高中数学 来源: 题型:
某市甲、乙两校高二级学生分别有1100人和1000人,为了解两校全体高二级学生期末统考的数学成绩情况,采用分层抽样方法从这两所学校共抽取105名高二学生的数学成绩,并得到成绩频数分布表如下,规定考试成绩在[120,150]为优秀.
甲校:
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) | [110,120) | [120,130) | [130,140) | [140,150) |
| 频数 | 2 | 3 | 10 | 15 | 15 | x | 3 | 1 |
乙校:
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) | [110,120) | [120,130) | [130,140) | [140,150) |
| 频数 | 1 | 2 | 9 | 8 | 10 | 10 | y | 3 |
(1)求表中x与y的值;
(2)由以上统计数据完成下面2x2列联表,问是否有99%的把握认为学生数学成绩优秀与所在学校有关?
| 甲校 | 乙校 | 总计 | |
| 优秀 | a | b | a+b |
| 非优秀 | c | d | c+d |
| 总计 | a+c | b+d | n |
参考公式:![]()
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源:2013年广东省湛江市高考数学二模试卷(文科)(解析版) 题型:解答题
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) | [110,120) | [120,130) | [130,140) | [140,150) |
| 频数 | 2 | 3 | 10 | 15 | 15 | x | 3 | 1 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) | [110,120) | [120,130) | [130,140) | [140,150) |
| 频数 | 1 | 2 | 9 | 8 | 10 | 10 | y | 3 |
| 甲校 | 乙校 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com