
【题目】若定义在![]() 上的函数
上的函数![]() ,
,![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若![]() ,
,![]() ,
,![]() 满足
满足![]() ,则称
,则称![]() 比
比![]() 更接近
更接近![]() .当
.当![]() 且
且![]() 时,试比较
时,试比较![]() 和
和![]() 哪个更接近
哪个更接近![]() ,并说明理由.
,并说明理由.
【答案】(1)当![]() 时,
时, ![]() 单调递增区间为
单调递增区间为![]() ;当
;当![]() 时,
时, ![]() 单调递增区间为
单调递增区间为![]() ,
,![]() 单调递减区间为
单调递减区间为![]() ;(2)
;(2)![]() 比
比![]() 更接近
更接近![]() ,理由见解析.
,理由见解析.
【解析】
(1)对![]() 求导,分
求导,分![]() 和
和![]() 进行讨论,研究
进行讨论,研究![]() 的正负情况,从而得到
的正负情况,从而得到![]() 的单调区间;(2)设
的单调区间;(2)设![]() ,
,![]() ,
,
利用导数研究出![]() 和
和![]() 在
在![]() 的单调性和正负情况,分
的单调性和正负情况,分![]() 和
和![]() 进行讨论,得到
进行讨论,得到![]() 和
和![]() 的大小关系,从而得到答案.
的大小关系,从而得到答案.
(1)函数![]() ,
,
求导得到![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,由
时,由![]() ,得到
,得到![]() ,
,
所以![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
综上所述,当![]() 时,
时, ![]() 单调递增区间为
单调递增区间为![]() ;当
;当![]() 时,
时, ![]() 单调递增区间为
单调递增区间为![]() ,
,![]() 单调递减区间为
单调递减区间为![]() ;
;
(2)设![]() ,
,![]()
所以![]() ,所以
,所以![]() 在
在![]() 时单调递减,
时单调递减,
又因为![]()
所以当![]() 时
时![]() ,当
,当![]() 时,
时,![]() .
.
而![]() ,设
,设![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上单调递增,即
上单调递增,即![]() 在
在![]() 上单调递增,
上单调递增,
而![]() ,所以
,所以![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 时单调递增,且
时单调递增,且![]() ,
,
所以![]() .
.
①当![]() 时
时![]() ,
,
设![]() ,则
,则![]()
所以![]() 在
在![]() 单调递减,
单调递减,![]() .
.
又因为![]() ,所以
,所以![]() ,
,
所以![]()
所以![]() 比
比![]() 更接近
更接近![]() .
.
②当![]() 时,
时,![]() ,
, ![]() ,
,
设![]() ,则
,则![]() ,
,
设![]() ,
,![]() ,
,
所以![]() 在
在![]() 上单调递减,即
上单调递减,即![]() 在
在![]() 上单调递减,
上单调递减,
所以![]()
所以![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,即
,即![]() ,
,
所以![]() 比
比![]() 更接近
更接近![]() .
.
综上所述,当![]() 且
且![]() 时,
时,![]() 比
比![]() 更接近
更接近![]() .
.


科目:高中数学 来源: 题型:
【题目】已知某校甲、乙、丙三个兴趣小组的学生人数分别为36,24,12.现采用分层抽样的方法从中抽取6人,进行睡眠质量的调查.
(1)应从甲、乙、丙三个兴趣小组的学生中分别抽取多少人?
(2)设抽出的6人分别用![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 表示,现从6人中随机抽取2人做进一步的身体检查.
表示,现从6人中随机抽取2人做进一步的身体检查.
(i)试用所给字母列出所有可能的抽取结果;
(ii)设![]() 为事件“抽取的2人来自同一兴趣小组”,求事件
为事件“抽取的2人来自同一兴趣小组”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】明初出现了一大批杰出的骑兵将领,比如徐达、常遇春、李文忠、蓝玉和朱棣.明初骑兵军团击败了不可一世的蒙古骑兵,是当时世界上最强骑兵军团.假设在明军与元军的某次战役中,明军有8位将领,善用骑兵的将领有5人;元军有8位将领,善用骑兵的有4人.
(1)现从明军将领中随机选取4名将领,求至多有3名是善用骑兵的将领的概率;
(2)在明军和元军的将领中各随机选取2人,![]() 为善用骑兵的将领的人数,写出
为善用骑兵的将领的人数,写出![]() 的分布列,并求
的分布列,并求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和为Sn,若对任意正整数n,总存在正整数m,使得Sn=am,则称数列{an}为S数列.
(1)S数列的任意一项是否可以写成其某两项的差?请说明理由.
(2)①是否存在等差数列为S数列,若存在,请举例说明;若不存在,请说明理由.
②是否存在正项递增等比数列为S数列,若存在,请举例说明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某产品的三个质量指标分别为x, y, z, 用综合指标S =" x" + y + z评价该产品的等级. 若S≤4, 则该产品为一等品. 现从一批该产品中, 随机抽取10件产品作为样本, 其质量指标列表如下:
产品编号 | A1 | A2 | A3 | A4 | A5 |
质量指标(x, y, z) | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
产品编号 | A6 | A7 | A8 | A9 | A10 |
质量指标(x, y, z) | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
(Ⅰ) 利用上表提供的样本数据估计该批产品的一等品率;
(Ⅱ) 在该样品的一等品中, 随机抽取两件产品,
(1) 用产品编号列出所有可能的结果;
(2) 设事件B为 “在取出的2件产品中, 每件产品的综合指标S都等于4”, 求事件B发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学大学毕业后,决定利用所学专业进行自主创业,经过市场调查,生产一小型电子产品需投入固定成本2万元,每生产![]() 万件,需另投入流动成本
万件,需另投入流动成本![]() 万元,当年产量小于
万元,当年产量小于![]() 万件时,
万件时,![]() (万元);当年产量不小于7万件时,
(万元);当年产量不小于7万件时,![]() (万元).已知每件产品售价为6元,假若该同学生产的商品当年能全部售完.
(万元).已知每件产品售价为6元,假若该同学生产的商品当年能全部售完.
(1)写出年利润![]() (万年)关于年产量
(万年)关于年产量![]() (万件)的函数解析式;(注:年利润=年销售收入-固定成本-流动成本)
(万件)的函数解析式;(注:年利润=年销售收入-固定成本-流动成本)
(2)当年产量约为多少万件时,该同学的这一产品所获年利润最大?最大年利润是多少?
(取![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已如椭圆E:![]() (
(![]() )的离心率为
)的离心率为![]() ,点
,点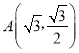 在E上.
在E上.
(1)求E的方程:
(2)斜率不为0的直线l经过点![]() ,且与E交于P,Q两点,试问:是否存在定点C,使得
,且与E交于P,Q两点,试问:是否存在定点C,使得![]() ?若存在,求C的坐标:若不存在,请说明理由
?若存在,求C的坐标:若不存在,请说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从0,1,2,3,4这五个数中任选三个不同的数组成一个三位数,记X为所组成的三位数各位数字之和.
(1)求X是奇数的概率;
(2)求X的概率分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的参数方程是 (φ为参数,a>0),直线l的参数方程是
(φ为参数,a>0),直线l的参数方程是![]() (t为参数),曲线C与直线l有一个公共点在x轴上,以坐标原点为极点,x轴的正半轴为极轴建立坐标系.
(t为参数),曲线C与直线l有一个公共点在x轴上,以坐标原点为极点,x轴的正半轴为极轴建立坐标系.
(1)求曲线C的普通方程;
(2)若点A(ρ1,θ),B(ρ2,θ+![]() ),C(ρ3,θ+
),C(ρ3,θ+![]() )在曲线C上,求
)在曲线C上,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com