
【题目】已知点![]() 是椭圆
是椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 是该椭圆上一点,若当
是该椭圆上一点,若当![]() 时,
时,![]() 面积达到最大,最大值为
面积达到最大,最大值为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() 为坐标原点,是否存在过左焦点
为坐标原点,是否存在过左焦点![]() 的直线
的直线![]() ,与椭圆交于
,与椭圆交于![]() 两点,使得
两点,使得![]() 的面积为
的面积为![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
【题目】为了迎接2019年全国文明城市评比,某市文明办对市民进行了一次文明创建知识的网络问卷调查.每一位市民有且仅有一次参加机会,通过随机抽样,得到参加问卷调查的1000人的得分(满分:100分)数据,统计结果如下表所示:
组别 |
|
|
|
|
|
|
|
频数 | 25 | 150 | 200 | 250 | 225 | 100 | 50 |
(1)由频数分布表可以认为,此次问卷调查的得分![]() 服从正态分布
服从正态分布![]() ,
,![]() 近似为这1000人得分的平均值(同一组数据用该组区间的中点值作为代表),请利用正态分布的知识求
近似为这1000人得分的平均值(同一组数据用该组区间的中点值作为代表),请利用正态分布的知识求![]() ;
;
(2)在(1)的条件下,文明办为此次参加问卷调查的市民制定如下奖励方案:
(i)得分不低于![]() 的可以获赠2次随机话费,得分低于
的可以获赠2次随机话费,得分低于![]() 的可以获赠1次随机话费;
的可以获赠1次随机话费;
(ii)每次获赠的随机话费和对应的概率为:
获赠的随机话费(单位:元) | 20 | 40 |
概率 |
|
|
现市民小王要参加此次问卷调查,记![]() (单位:元)为该市民参加问卷调查获赠的话费,求
(单位:元)为该市民参加问卷调查获赠的话费,求![]() 的分布列及数学期望.
的分布列及数学期望.
附:①![]() ;
;
②若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() ,
,![]() ,
,![]() 分别为椭圆的右顶点,上顶点和右焦点,且
分别为椭圆的右顶点,上顶点和右焦点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)![]() ,
,![]() 是椭圆上的两个动点,若直线
是椭圆上的两个动点,若直线![]() 与直线
与直线![]() 的斜率之和为
的斜率之和为![]() ,证明,直线
,证明,直线![]() 恒过定点.
恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第十三届全国人大第二次会议于2019年3月5日在北京开幕.为广泛了解民意,某人大代表利用网站进行民意调查.数据调查显示,民生问题是百姓最为关心的热点,参与调查者中关注此问题的约占![]() .现从参与调查者中随机选出200人,并将这200人按年龄分组,第1组
.现从参与调查者中随机选出200人,并将这200人按年龄分组,第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
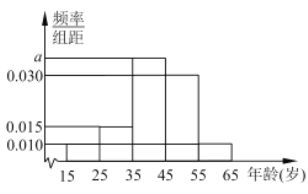
(1)求![]() ;
;
(2)现在要从年龄较小的第1组和第2组中用分层抽样的方法抽取5人,并再从这5人中随机抽取2人接受现场访谈,求这两人恰好属于不同组别的概率;
(3)把年龄在第1,2,3组的居民称为青少年组,年龄在第4,5组的居民称为中老年组,若选出的200人中不关注民生问题的中老年人有10人,问是否有![]() 的把握认为是否关注民生与年龄有关?
的把握认为是否关注民生与年龄有关?
附:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
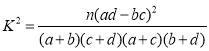 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.命题“![]() ”的否定是“
”的否定是“![]() ”
”
B.命题“已知![]() ,若
,若![]() 则
则![]() 或
或![]() ”是真命题
”是真命题
C.命题“若![]() 则函数
则函数![]() 只有一个零点”的逆命题为真命题
只有一个零点”的逆命题为真命题
D.“![]() 在
在![]() 上恒成立”
上恒成立”![]() 在
在![]() 上恒成立
上恒成立
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极点与平面直角坐标系的原点重合,极轴与![]() 轴的正半轴重合,直线
轴的正半轴重合,直线![]() 的参数方程为
的参数方程为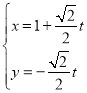 (
(![]() 是参数),曲线
是参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 为曲线
为曲线![]() 上一点,求使
上一点,求使![]() 面积取得最大值时的
面积取得最大值时的![]() 点坐标.
点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题正确的是( )
A.若一个平面内由无穷多个点到另一个平面的距离相等,则这两个平面平行;
B.一个平面内的两条相交直线与另一个平面内的两条相交直线分别垂直,则这两个平面垂直;
C.若一个平面内有3条两两不平行的直线与另一个平面所成角均相等,则这两个平面平行;
D.若两个平面相交,则一个平面内不存在不共线三点到另一个平面距离相等.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现安排6名同学前往4所学校进行演讲,要求甲、乙两同学不能前往同一个学校,每个学校都有人前往,每人只前往一个学校,则满足上述要求的不同安排方案数为________.(用数字作答)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com