
如图所示,已知PA与⊙O相切,A为切点,PBC为割线,CD∥AP,AD与BC相交于点E,F为CE上一点,且DE2=EF·EC.
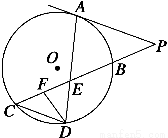
(1)求证:∠P=∠EDF;
(2)求证:CE·EB=EF·EP;
(3)若CE∶BE=3∶2,DE=6,EF=4,求PA的长.
(1) (2)见解析 (3) 
【解析】
(1)证明 ∵DE2=EF·EC,∴DE∶CE=EF∶ED.
∵∠DEF是公共角,∴△DEF∽△CED.
∴∠EDF=∠C.
∵CD∥AP,∴∠C=∠P.
∴∠P=∠EDF.
(2)证明 ∵∠P=∠EDF,∠DEF=∠PEA,
∴△DEF∽△PEA.
∴DE∶PE=EF∶EA.即EF·EP=DE·EA.
∵AD、BC相交于点E,
∴DE·EA=CE·EB.∴CE·EB=EF·EP.
(3)解 ∵DE2=EF·EC,DE=6,EF=4,∴EC=9.
∵CE∶BE=3∶2,∴BE=6.
∵CE·EB=EF·EP,∴9×6=4×EP.
解得:EP= .
.
∴PB=PE-BE= ,PC=PE+EC=
,PC=PE+EC= .
.
由切割线定理得:PA2=PB·PC,
∴PA2=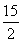 ×
× ,
,
∴PA=
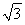 .
.


科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第七章第2课时练习卷(解析版) 题型:填空题
设函数f0(x)=1-x2,f1(x)=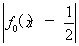 ,fn(x)=
,fn(x)=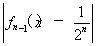 ,(n≥1,n≥N),则方程f1(x)=
,(n≥1,n≥N),则方程f1(x)=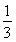 有________个实数根,方程fn(x)=
有________个实数根,方程fn(x)=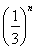 有________个实数根.
有________个实数根.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第一章第2课时练习卷(解析版) 题型:解答题
已知f(x)=x+ -3,x∈[1,2].
-3,x∈[1,2].
(1)当b=2时,求f(x)的值域;
(2)若b为正实数,f(x)的最大值为M,最小值为m,且满足M-m≥4,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第一章第1课时练习卷(解析版) 题型:填空题
已知集合A={1,2,3,4,5},B={(x,y)|x∈A,y∈A,x-y∈A},则B中元素的个数为________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第一章第1课时练习卷(解析版) 题型:解答题
已知集合A={x|ax2-3x+2=0,a∈R}.
(1) 若A是空集,求a的取值范围;
(2) 若A中只有一个元素,求a的值,并将这个元素写出来;
(3) 若A中至多有一个元素,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高中数学人教A版选修4-1达标演练模块检测练习卷(解析版) 题型:填空题
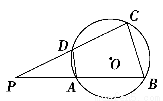
如图所示,四边形ABCD内接于⊙O,AD∶BC=1∶2,AB=35,PD=40,则过点P的⊙O的切线长是________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高中数学人教A版选修4-1达标演练模块检测练习卷(解析版) 题型:选择题
如图,AB为⊙O直径,MN切⊙O于C,AC= BC,则sin∠MCA=
BC,则sin∠MCA=

A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高中数学人教A版选修4-1达标检测第2讲练习卷(解析版) 题型:选择题
如图所示,PA切圆于A,PA=8,直线PCB交圆于C、B,连接AB、AC,且PC=4,AD⊥BC于D,∠ABC=α,∠ACB=β,则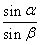 的值等于
的值等于
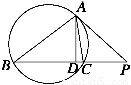
A.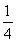 B.
B.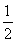 C.2 D.4
C.2 D.4
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高中数学人教A版选修4-1知能达标2-4练习卷(解析版) 题型:解答题
(拓展深化)如图所示,△ABC内接于⊙O,AB=AC,直线XY切⊙O于点C,BD∥XY,AC、BD相交于E.
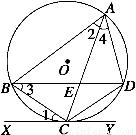
(1)求证:△ABE≌△ACD;
(2)若AB=6 cm,BC=4 cm,求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com