
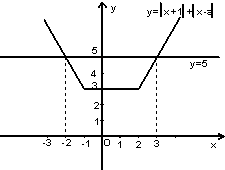
|
| 3 |
| 6 |
|
| 3 |
| x′ |
| 2 |
| y′ | ||
|
| x2 |
| 4 |
| y2 |
| 3 |
|
| 3 |
| 3 |
| 6 |
|2
| ||||||
|
|2
| ||||||
|
| 42 |
| π |
| 4 |
| 2 |
| ||
| 2 |
|


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源: 题型:
 本题有(1),(2),(3)三个选答题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题计分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑.
本题有(1),(2),(3)三个选答题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题计分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑.
|
|
| b 2 |
| 4 |
| c 2 |
| 9 |
| b 2 |
| 4 |
| c 2 |
| 9 |
| (a+b+c) 2 |
| 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
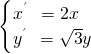 下圆x2+y2=1变为曲线C.求曲线C的方程,并指出曲线的类型;当曲线C的动点M到直线L:
下圆x2+y2=1变为曲线C.求曲线C的方程,并指出曲线的类型;当曲线C的动点M到直线L: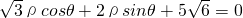 距离的最大值时,求点M的坐标.
距离的最大值时,求点M的坐标.查看答案和解析>>
科目:高中数学 来源:2010年福建省漳州市漳浦县达志中学高考数学模拟试卷(理科)(解析版) 题型:解答题
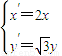 下圆x2+y2=1变为曲线C.求曲线C的方程,并指出曲线的类型;当曲线C的动点M到直线L:
下圆x2+y2=1变为曲线C.求曲线C的方程,并指出曲线的类型;当曲线C的动点M到直线L: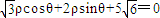 距离的最大值时,求点M的坐标.
距离的最大值时,求点M的坐标.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com