
【题目】如图,已知矩形ABCD所在平面与等腰直角三角形BEC所在平面互相垂直,BE⊥EC,AB=BE,M为线段AE的中点.
(Ⅰ) 证明:BM⊥平面AEC;
(Ⅱ) 求MC与平面DEC所成的角的余弦值.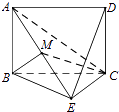
【答案】证明:(Ⅰ)因为平面ABCD⊥平面BEC,
所以AB⊥平面BEC,故AB⊥EC.
因为BE⊥EC,所以EC⊥平面ABE,
故EC⊥BM.
因为AB=BE,M为AE的中点,所以AE⊥BM.
所以BM⊥平面AEC.
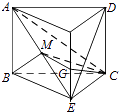
解:(Ⅱ)如图,将几何体ABCDE补成三棱柱AFD﹣BEC,
设EF的中点为G,连结MG,GC.
因为MG∥BE,所以MG⊥平面DEC.
因此∠MCG为MC与平面DEC所成的角.
不妨设AB=2,则AB=BE=EC=2,
因此MG=1, ![]() ,
, ![]() ,
,
故 ![]() ,
,
所以MC与平面DEC所成的角的余弦值为 ![]() .
.
【解析】(Ⅰ)由已知推导出AB⊥EC,EC⊥BM,AE⊥BM,由此能证明BM⊥平面AEC.(Ⅱ)将几何体ABCDE补成三棱柱AFD﹣BEC,设EF的中点为G,连结MG,GC,推导出∠MCG为MC与平面DEC所成的角,由此能求出MC与平面DEC所成的角的余弦值.
【考点精析】本题主要考查了直线与平面垂直的判定和空间角的异面直线所成的角的相关知识点,需要掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则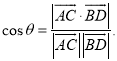 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】一个正三角形等分成4个全等的小正三角形,将中间的一个正三角形挖掉(如图1),再将剩余的每个正三角形分成4个全等的小正三角形,并将中间的一个正三角形挖掉,得图2,如此继续下去… 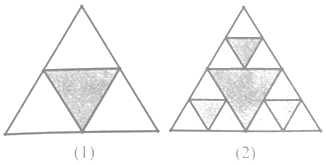
(1)图3共挖掉多少个正三角形?
(2)设原正三角形边长为a,第n个图形共挖掉多少个正三角形?这些正三角形面积和为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三角形ABC的顶点坐标为A(﹣1,5)、B(﹣2,﹣1)、C(4,3).
(1)求AB边上的高线所在的直线方程;
(2)求三角形ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2x+t,g(x)=x2﹣t(t∈R)
(1)当x∈[2,3]时,求函数f(x)的值域(用t表示)
(2)设集合A={y|y=f(x),x∈[2,3]},B={y|y=|g(x)|,x∈[2,3]},是否存在正整数t,使得A∩B=A.若存在,请求出所有可能的t的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市规定,高中学生在校期间须参加不少于80小时的社区服务才合格.某校随机抽取20位学生参加社区服务的数据,按时间段[75,80),[80,85),[85,90),[90,95),[95,100](单位:小时)进行统计,其频率分布直方图如图所示. 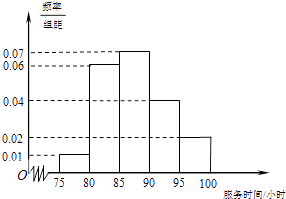
(1)求抽取的20人中,参加社区服务时间不少于90小时的学生人数;
(2)从参加社区服务时间不少于90小时的学生中任意选取2人,求所选学生的参加社区服务时间在同一时间段内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知动点
中,已知动点![]() 到定点
到定点![]() 的距离与到定直线
的距离与到定直线![]() 的距离之比为
的距离之比为![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)已知![]() 为定直线
为定直线![]() 上一点.
上一点.
①过点![]() 作
作![]() 的垂线交轨迹
的垂线交轨迹![]() 于点
于点![]() (
(![]() 不在
不在![]() 轴上),求证:直线
轴上),求证:直线![]() 与
与![]() 的斜率之积是定值;
的斜率之积是定值;
②若点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作动直线
作动直线![]() 交轨迹
交轨迹![]() 于不同两点
于不同两点![]() ,线段
,线段![]() 上的点
上的点![]() 满足
满足![]() ,求证:点
,求证:点![]() 恒在一条定直线上.
恒在一条定直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某景区修建一栋复古建筑,其窗户设计如图所示.圆![]() 的圆心与矩形
的圆心与矩形![]() 对角线的交点重合,且圆与矩形上下两边相切(
对角线的交点重合,且圆与矩形上下两边相切(![]() 为上切点),与左右两边相交(
为上切点),与左右两边相交(![]() ,
, ![]() 为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1m,且
为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1m,且![]() .设
.设![]() ,透光区域的面积为
,透光区域的面积为![]() .
.
(1)求![]() 关于
关于![]() 的函数关系式,并求出定义域;
的函数关系式,并求出定义域;
(2)根据设计要求,透光区域与矩形窗面的面积比值越大越好.当该比值最大时,求边![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
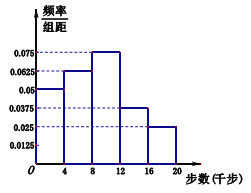
【题目】微信运动和运动手环的普及,增强了人民运动的积极性,每天一万步称为一种健康时尚,某中学在全校范围内内积极倡导和督促师生开展“每天一万步”活动,经过几个月的扎实落地工作后,学校想了解全校师生每天一万步的情况,学校界定一人一天走路不足![]() 千步为不健康生活方式,不少于
千步为不健康生活方式,不少于![]() 千步为超健康生活方式者,其他为一般生活方式者,学校委托数学组调查,数学组采用分层抽样的办法去估计全校师生的情况,结合实际及便于分层抽样,认定全校教师人数为
千步为超健康生活方式者,其他为一般生活方式者,学校委托数学组调查,数学组采用分层抽样的办法去估计全校师生的情况,结合实际及便于分层抽样,认定全校教师人数为![]() 人,高一学生人数为
人,高一学生人数为![]() 人,高二学生人数
人,高二学生人数![]() 人,高三学生人数
人,高三学生人数![]() ,从中抽取
,从中抽取![]() 人作为调查对象,得到了如图所示的这
人作为调查对象,得到了如图所示的这![]() 人的频率分布直方图,这
人的频率分布直方图,这![]() 人中有
人中有![]() 人被学校界定为不健康生活方式者.
人被学校界定为不健康生活方式者.
(1)求这次作为抽样调查对象的教师人数;
(2)根据频率分布直方图估算全校师生每人一天走路步数的中位数(四舍五入精确到整数步);
(3)校办公室欲从全校师生中速记抽取![]() 人作为“每天一万步”活动的慰问对象,计划学校界定不健康生活方式者鞭策性精神鼓励
人作为“每天一万步”活动的慰问对象,计划学校界定不健康生活方式者鞭策性精神鼓励![]() 元,超健康生活方式者表彰奖励
元,超健康生活方式者表彰奖励![]() 元,一般生活方式者鼓励性奖励
元,一般生活方式者鼓励性奖励![]() 元,利用样本估计总体,将频率视为概率,求这次校办公室慰问奖励金额恰好为
元,利用样本估计总体,将频率视为概率,求这次校办公室慰问奖励金额恰好为![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市司法部门为了宣传《宪法》举办法律知识问答活动,随机对该市18~68岁的人群抽取一个容量为n的样本,并将样本数据分成五组:[18,28),[28,38),[38,48),[48,58),[58,68),再将其按从左到右的顺序分别编号为第1组,第2组,…,第5组,绘制了样本的频率分布直方图;并对回答问题情况进行统计后,结果如下表所示.
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的比例 |
第1组 | [18,28) | 5 | 0.5 |
第2组 | [28,38) | 18 | a |
第3组 | [38,48) | 27 | 0.9 |
第4组 | [48,58) | x | 0.36 |
第5组 | [58,68) | 3 | 0.2 |
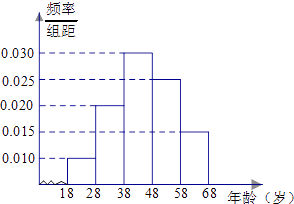
(1)分别求出a,x的值;
(2)从第2,3,4组回答正确的人中用分层抽样方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,决定在所抽取的6人中随机抽取2人颁发幸运奖,求:所抽取的人中第2组至少有1人获得幸运奖的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com