练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知O是四边形ABCD内一点，若+++=0，则：

    ①四边形ABCD为正方形，点O是正方形ABCD的中心；②四边形ABCD为一般四边形，点O是其对角线交点；③四边形ABCD为一般四边形，点O是其外接圆圆心；④四边形ABCD为一般四边形，点O是其对边中点连线的交点．

    上述说法正确的是_____________．（填序号）

    答案：④

    解析：由+++=0，则+=-（+），若设E、F分别为AB、CD中点，则+=2，+=2 ，?∴=-，即E、O、F三点共线，且O为EF中点.由任意四边形四边中点连线为平行四边形和O为两组对边中点的连线的交点.故④正确.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

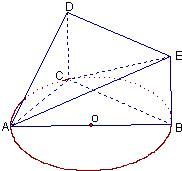    精英家教网如图，△ABC内接于圆O，AB是圆O的直径，四边形DCBE为平行
    四边形，DC⊥平面ABC，AB=2，已知AE与平面ABC所成的角为θ，
    且tanθ=
    		3
    2
    ．
    （1）证明：平面ACD⊥平面ADE；
    （2）记AC=x，V（x）表示三棱锥A-CBE的体积，求V（x）的表达式；
    （3）当V（x）取得最大值时，求二面角D-AB-C的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （1）自圆O外一点P引切线与圆切于点A，M为PA中点，过M引割线交圆于B，C两点．求证：∠MCP=∠MPB．
    （2）在平面直角坐标系xOy中，已知四边形ABCD的四个顶点A（0，1），B（2，1），C（2，3），D（0，2），经矩阵M=
    10
    k1
    表示的变换作用后，四边形ABCD变为四边形A1B1C1D1，问：四边形ABCD与四边形A1B1C1D1的面积是否相等？试证明你的结论．
    （3）已知A是曲线ρ=12sinθ上的动点，B是曲线ρ=12cos(θ-
    π
    6
    )    上的动点，试求AB的最大值．
    （4）设p是△ABC内的一点，x，y，z是p到三边a，b，c的距离，R是△ABC外接圆的半径，证明
    		x
    +
    		y
    +
    		z
    ≤
    1
    		2R
    		a2+b2+c2
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    精英家教网如图，已知BC是半径为1的半圆O的直径，A是半圆周上不同于B，C的点，又DC⊥面ABC，四边形ACDE为梯形，DE∥AC，且AC=2DE，DC=2，二面角B-DE-C的大小为θ，tanθ=
    34

    （1）证明：面ABE⊥面ACDE；
    （2）求四棱锥B-ACDE的体积．

    查看答案和解析>>

    科目：高中数学 来源：2010年江西上高二中、新余钢铁中学高三年级全真模拟数学（理科）试题 题型：解答题

    如图，△ABC内接于圆O,AB是圆O的直径，四边形DCBE为平行四边形，DC平面ABC ,，已知AE与平面ABC所成的角为,且．

       （1）证明：平面ACD平面；

       （2）记，表示三棱锥A－CBE的体积，求的表达式；

       （3）当取得最大值时，求二面角D－AB－C的大小．

     

    查看答案和解析>>

    科目：高中数学 来源：0103 期末题 题型：解答题

    如图，△ABC内接于圆O，AB是圆O的直径，四边形DCBE为平行四边形，DC⊥平面ABC，AB=2，已知AE与平面ABC所成的角为θ，且tanθ=。
    （Ⅰ）证明：平面ACD⊥平面ADE；
    （Ⅱ）记AC=x，V(x)表示三棱锥A-CBE的体积，求V(x)的表达式；
    （Ⅲ）当V(x)取得最大值时，求二面角D-AB-C的大小。

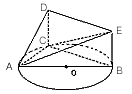
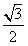    查看答案和解析>>

    同步练习册答案